Actions from predictions
A general framework for outcome maximization. Is this reinforcement learning?
This is a live blog of Lecture 20 of the 2025 edition of my graduate machine learning class “Patterns, Predictions, and Actions.” A Table of Contents is here.
Last time, we looked at the problem of experiment design as maximizing average outcomes. The goal was to find the best treatment for a population of individuals. The strategies I proposed reduced to a two-stage process: experimentation followed by policy implementation. I defined the quality of the solution by comparing it to the counterfactual where you knew the best policy in advance.
This class of problems can be defined more broadly and quickly take on a flavor of machine learning. Again, consider a population of individuals for whom we can recommend an action. Today, let’s also allow a new component, a set of features defining each individual. We would like to find the actions customized to these features that maximize the average outcome for the population. If you’d prefer this as an equation:
As a baseline for comparison, we can define a counterfactually optimal solution. Let’s say we know all of the problem details in advance, but require that the action be the same for every individual with the same features. We analyzed this problem way back in Lecture 2, and saw that it amounted to solving a bunch of problems for each unique value of the features.
This average outcome optimization problem was the original motivation for machine learning. Our idea was that if we could gather representative data, we could estimate predictions or actions that would maximize outcomes, and then apply them more generally, hoping that the new data would be the same as the old. The formulation we’re studying today makes the population evaluation explicit.
This general problem doesn’t have a tidy analysis like we saw for experiment design, but there are three strategies you can readily apply. The first is again experiment and then decide. Gather a random sample of individuals, and fit the relationship between action and outcome using machine learning of some kind. Then declare the policy is to take the action that maximizes this estimated outcome for each individual.1 This policy makes sense and is what we mostly do in practice in machine learning.
Unfortunately, there are only a few special cases where people have derived nice mathematical analyses of this strategy. You need some notion of what machine learning theorists call “sample complexity,” a measure of estimating one’s prediction error from a random sample. Actionable sample complexity bounds are hard to compute even for simple linear models. And even when there is structure, you tend to need more math than you’d like to get “optimal” algorithms.
The experiment design problem from Lecture 19 was a special case of this problem. There, we assumed there were no distinguishing features for individuals. We restricted the actions to be binary. Unfortunately, even there, a clean analysis of a simple adaptive strategy took a few pages of math and some ugly probability manipulation.
To avoid this mathematical complexity, it’s often easier to analyze the problem as a sequence of tiny experiments where you take a small batch of examples each time and update your predictions accordingly. This is the second strategy. For example, suppose we restrict our attention to actions being linear functions of the features, our outcomes are simple binary values, and we assume there is some counterfactual outcome that achieves an average outcome of 1. Then we can apply the Perceptron algorithm to this problem, updating our working action with each example. Using the analysis from Lecture 7, the gap between the counterfactual outcome and the Perceptron is upper-bounded by a constant divided by N.
We can extend this incremental learning idea to the case where the outcome function is known and differentiable. For linear models and concave objectives, we can run the incremental gradient method and apply the gap bound we derived in Lecture 11. Now the gap will be upper-bounded by a constant divided by the square root of N. Though we can’t get clean guarantees, the incremental gradient method can also be applied when the outcomes are differentiable and the action is a differentiable function of the features, be it a neural net or whatever else.
Along these lines, another special case of the problem here is just general iterative optimization. We want to minimize a function with respect to some decision variable, but we can change that decision variable at each iteration. The gap is the average error between the iterates and the optimum. If you have an algorithm that works well when the function can vary at each iteration, you also have a decent algorithm for optimization. This is the motivation for the field of online optimization. Keep this in mind when we come back to cover reinforcement learning on LLMs.
The third and final strategy is a mix of the two prior. It’s called the greedy method. Here, to determine the action for the next individual in our queue, we would estimate their outcome by running a learning algorithm on all the data we’ve collected so far. This method performs well in practice, and, with the right assumptions, in theory too. You can think of it as a variant of the common industrial machine learning practice of continually retraining models on the deluge of new data collected every day.
A closing note. I went out of my way in this post and the last to avoid a lot of unsavory terminology from the academic literature on these problems. It’s unfortunate, especially so given our cultural climate, that outcome optimization is always described in terms of gambling. It’s such unpleasant words to have to say to discuss a legitimately important and practical problem. The problem we described last time is commonly called a “multi-armed bandit,” as it models finding the slot machine with the best return. The problem we talked about today is “the contextual bandit.” The gap between a policy and its counterfactual outcome is called “regret,” which all gamblers have. Experimentation is called “exploration.” Policy is called “exploitation.” They want to replace “p-values” with “bets.” That’s not an improvement! I’m going out of my way to avoid using their terms. You shouldn’t have to use them either.
Or, if you’re a sicko, sample the action from the Boltzmann distribution induced by the estimated outcomes.


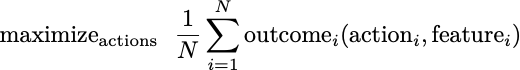
What's the problem with gambling terms?
I have really enjoyed the pdf document with ugly(!) math. Thanks so much for such a clear and readable exposition.
I am thinking that equations (11) and (12) are missing the outcome variables y_i(z_i) so that the mean of their difference can be associated with ATE. Am I correct?