Minimal Theory
What are the most important lessons from optimization theory for machine learning?
This is a live blog of Lecture 11 of the 2025 edition of my graduate machine learning class “Patterns, Predictions, and Actions.” A Table of Contents is here.
Entire books have been written on the analysis of stochastic gradient descent, but today I’ll give a condensed 90-minute tutorial on what I find most relevant and justifiable in machine learning. This semester, I’m working hard to only present the justifiable parts. What can we say that is true and testable? For optimization of linear prediction functions and convex losses, you can say a lot, and it’s important not to lose sight of this.
Machine learning theory is confusing because anything that relies on how data is distributed, such as assumptions about functional form or probabilistic relations between data points, cannot be verified. However, in optimization, the model of a linear function and a convex loss is under the data analyst’s control. You don’t have to use linear predictors, but if you do, optimization can make you verifiable guarantees. The value of these guarantees in a larger machine learning pipeline is a separate question.
For an introduction to optimization, I wanted something that paralleled the study of the perceptron. Stochastic gradient descent on convex loss functions for linear predictors in binary classification (yes, a mouthful) looks very much like the perceptron update. To see the relationship, let’s use a little mathematical notation. Let x denote the feature vector, y the label (equal to 1 or -1), w the weights, and p = <x,w> the prediction. Then, a stochastic gradient update takes the form
Here, t is a tunable stepsize parameter, and e(u) is some decreasing function that measures errors. For the perceptron, e(u) is equal to 1 when u is negative, 0 when u is nonnegative. For the support vector machine, e(u) is 1 when u-1 is negative, 0 otherwise. For the squared loss, e(u) = u-1. For logistic regression,
No matter which loss function you choose, stochastic gradient for linear classification problems is some variant of the perceptron.
The added algorithmic generality does buy us some nice properties over the perceptron. For example, if you use the squared loss on separable data, you can predict exactly which set of weights this algorithm is converging to, even if there is an infinite set of minimizers. You can easily bound the rate at which it converges to this solution as well. Perceptron-like algorithms naturally handle the problem of overparameterized models and give a simple demonstration of how overparameterization does not impede out-of-sample generalization.
Stochastic gradient analysis is also easy to extend to nonseparable data, allowing you to understand how the perceptron and its variants converge when the data is not perfectly separable. Moreover, you can estimate this convergence without making any probabilistic assumptions about the data.1 Just like with the perceptron, you can convert a nonstochastic analysis into a generalization bound by making probabilistic assumptions about the data-generating process. This is an example of the power of “online-to-batch conversion,” linking deterministic convergence analyses to stories about what the future might look like.
I can derive all of this in 90 minutes.
I like this set of topics because we observe similar phenomena when applying stochastic gradient methods to nonlinear prediction problems. Stochastic gradient methods applied to nonlinear prediction problems are undeniably successful. Overparameterized nonlinear models trained with a constant stepsize converge to zero loss. The choice of optimizer implicitly biases which nonlinear solution you find.
But, though we have some thoughts about it in the book, I decided this year not to speculate much about nonlinear theories of stochastic gradient descent. No matter how much I try to convince myself, I find nonlinear convergence analysis has the same verifiability issues that pop up when we make statistical assumptions about data. You can construct toy models where you can prove something about the dynamics of nonlinear optimization, but it’s never clear these models actually tell you anything about neural networks. I know many people will disagree with me. To those folks: if you come up with something that replaces ADAM as the default solver in PyTorch, then we can talk.
Because without that, I worry that nonlinear optimization theories are mostly irrelevant for machine learning anyway. Do we see interesting, nonlinear dynamics in Weights & Biases plots in real problems? Not really. The number goes down. But more importantly, we don’t care if you can find a global minimum of the training error. We care if you can find a global minimum of the test error.
The dirty secret of machine learning is the actual optimization problem we solve is minimizing the held-out sample error. We often do this by minimizing the training error, and thus linear optimization can play a role similar to that of approximation theory. It gives us a rough guide to practice. It shows us that minimizing training error is possible, that overparameterization does not prevent generalization, and that how you set up your optimization problem dictates which predictor you’ll find. The combination of the optimizer, the architecture, and the hyperparameters implicitly selects a model. These are good lessons.
But while linear models give us good reason to believe that minimizing training error is one way to get decent holdout error, it’s not the only way. As we’ll discuss on Thursday, we always pick the model that has the lowest test error, regardless of whether we have a theoretical justification for the method. In machine learning, we are allowed to do whatever we want to make the holdout error small. We find models by tuning the knobs at our disposal. We have no good theory for how to get the knobs to the best setting. We just try not to have too many knobs.
If it were up to me, I’d call the algorithm the Incremental Gradient Method, not Stochastic Gradient Descent. You don’t need randomness for the method to work, and it’s also not necessarily a descent method. But SGD is what everyone uses, so I stick with it.


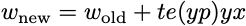
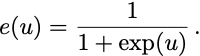
Yes, neural network training does indeed have fascinating non-linear optimization dynamics, if you know what to look for: https://centralflows.github.io/part1/.
"we always pick the model that has the lowest test error, regardless of whether we have a theoretical justification for the method. In machine learning, we are allowed to do whatever we want to make the holdout error small. "
Wouldn't this only apply to a single set of data? If the data is continuing to be added to the holdout data set, then won't the "best" minimum error fluctuate, whether the ML is run again on teh total of the old and new data, or just the original model run against the old holdout data plus the new data?