How to pick a sample size.
A brief introduction to adaptive experimentation without saying "exploration-exploitation tradeoff."
This is a live blog of Lecture 19 of the 2025 edition of my graduate machine learning class “Patterns, Predictions, and Actions.” A Table of Contents is here. For those interested in the gory mathematical details behind this post, here are some notes I wrote.
One of the pesky parts of randomized experiments is setting the sample size. It’s not desirable to constantly be experimenting on people. You want to have the smallest trials possible to ensure you satisfactorily determine the value of a treatment. What should this sample size be?
Let me try to pose a cost-benefit analysis. Assume we have a population of size N that might benefit from a treatment. From this population, we select a sample of size K uniformly at random. We run a randomized trial on this sample, and decide to accept or reject the treatment. We then apply this decision to the rest of the population. We record all of their outcomes and compute the average effect. If you prefer to see this as an equation:
To decide whether our aggregate outcome was good, we need to compare this average to something. One potential comparison is to think in the counterfactual manner of potential outcomes: what would have been the best single treatment to give to everyone if we knew in advance all of the outcomes? That is, we imagine a world in which we made a blanket recommendation to the entire population to either receive the treatment or not, and then figure out which recommendation would have led to a better average outcome. In equation form, the counterfactually optimal effect is
What is the gap between E and Ec? We can write this one out as an equation, too. If p denotes the probability that your randomized treatment assignment leads you to choose the suboptimal treatment recommendation, then the expected gap between the welfare under our decision making and the counterfactual effect is
Where ATE is the average treatment effect we studied in randomized trials. It is the average outcome under treatment minus the average outcome under control:
The gap G is at most equal to the magnitude of the average treatment effect. But it would be great if we could find a sample size, K, that makes this gap as small as possible.
In the world where the treatment is beneficial, the p in this expression is the probability that your statistical test recommends not accepting the treatment. This is the probability of a false negative. In statistical jargon, 1-p is called the power of your test. Similarly, when the treatment is harmful, p is the probability of mistakenly recommending it. This is the probability of a false positive. It is more or less the probability of incorrectly rejecting the null hypothesis.
A good experimenter should set the sample size so their test has adequate power. What should the sample size be? If you knew the size of your effect in advance (you never do), you could look up the appropriate sample size via a power calculation. To make the gap as small as possible, a reasonable power would be around 1-1/N.1 If you grind through the math, you’ll find you can get this when your sample size is roughly
For people who have seen rules of thumb for power calculations before, this should look familiar.
Unfortunately, this formula requires knowing the size of the treatment effect in advance of doing the experiment. That’s annoying. Statisticians and trialists know that this is just part of the elaborate theater you do when setting up an experiment. You guess the future to pick a sample size and hope for the best.
Now, if you are willing to do more than one experiment, there’s a neat trick to get around needing to know the treatment effect. Start with a reasonably large sample size and do a randomized trial.2 If the observed gap between the treatment and control is 1, meaning everyone has the same outcome, stop experimenting and assign everyone to the best outcome. If the measured gap is smaller, then do another experiment. For this trial, make your sample size four times larger and test for a gap half the size of the previous experiment. If this again fails to distinguish treatment from control, repeat the process. Quadruple the sample size, halve your decision threshold. If you repeat this process of successively increasing your sample size, you are guaranteed to have the same gap you would have achieved if you knew the treatment effect in advance.
This is the power of iterative experimentation. You can interpret this procedure as running increasingly large experiments until the confidence intervals around the treatment effect are bounded away from zero. The main difference from conventional experiments is that rather than having a p-value threshold of 0.05 and a power of 0.8, both error rates are set to optimal values to make good decisions in our metric. We keep our sample sizes small and still achieve an average benefit comparable to perfect experimentation. It’s sort of neat that if you can run multiple experiments, you don’t ever need to do power calculations.
Now, it’s not always practical to run experiments this way, as multiple stages mean trials will take much longer. You have to stage experiments sequentially, but that’s impractical when a single experiment takes multiple years. On the other hand, successive experimentation neuters the pedantic accusations that a study is underpowered.
Adaptive experiments are the first example of what you might call reinforcement learning in this class. I really don’t like the term “reinforcement learning,” for reasons I’ll expand on over the next few lectures. Sadly, I like the common name for the subfield of reinforcement learning focused on adaptive experimentation even less. People in the know call it “Bandits.” Ugh, the worst. The successive quadrupling algorithm I described today is an optimal algorithm for the stochastic multiarmed bandit problem. The gap we studied is usually called regret. I don’t like any of this terminology, and find both the terminology and the deluge of math in this field alienating. So I’m using this part of the class as an exercise to strip down the core concepts of adaptive experimentation and present them without too much excess baggage. Adaptive experimentation can be pretty useful and is much easier to implement than the literature suggests.
For most reasonable values of N, this is much larger than 80%. If you want to be a real nerd, then technically speaking, you can get away with a power of 1-1/(N|ATE|).
K=4 log(N) suffices here.



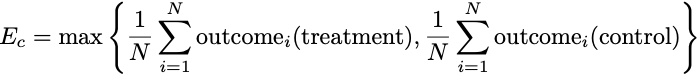
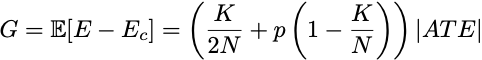
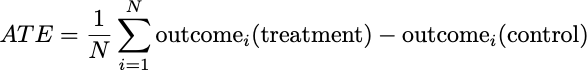
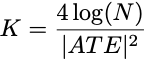
In practice, the anticipated treatment effect of a trial isn’t (shouldn’t be) entirely a guess. In trials of medical interventions, for example, researchers may be guided by the idea of a clinically significant effect size. This is based on existing understanding of the condition being treated and is the difference you would want to bring about for there to be a meaningful change in the condition’s effects or prognosis, such as improvement of x points on the main outcome measure. Still an elaborate theater, but with slightly less guesswork than you implied.
Another question: I don't understand the dimensions in the final formula for K. K and N are dimensionless, but ATE isn't? Something must be assumed about how we measure treatment effect. Is it binary?