Common Descent
Machine learning begins with the perceptron
This is a live blog of Lecture 7 of the 2025 edition of my graduate machine learning class “Patterns, Predictions, and Actions.” A Table of Contents is here.
So far in the class, we have only focused on optimization at the population level. We have asked what ideal predictions would look like given an evaluation framework and a population upon which we’ll be tested.
We now move to the trickier question: given a dataset of labeled individuals, how should you make predictions about populations you haven’t seen yet? That is, we are finally about to do some machine learning. Thanks for bearing with me.
Any introduction to machine learning has to start with the perceptron. The poor perceptron has been dumped on by AI researchers since Rosenblatt devised it in the 1950s. It was always just a cute trick that had nothing to do with intelligence. Such dismissals look pretty silly in 2025 when the only things that work in AI have their roots in perceptron learning rules.
The perceptron definitely feels too good to be true. It has the cleanest assumptions and some of the most robust algorithmic and extrapolative guarantees in all of machine learning. Most machine learning strives to be like the perceptron, but I know of no algorithm that is as simple to implement and analyze.
Let’s just go through the setup. We have data about a finite population of individuals. Each individual appears as a real-valued vector of attributes and a binary label. We assume that there exists a linear rule—one that weights each attribute and sums them up—which is positive on all individuals with label 1 and negative on all individuals with label -1.1 This assumption, called linear separability, means there is a linear classification rule that yields zero error on the population. In particular, it means that if two individuals have the same attribute vector, they necessarily must have the same label. This rules out many of the Meehlian actuarial applications such as medical testing. Separability is a big assumption, but let’s keep it for now and see where it takes us.
If you have linearly separable data, there is a remarkably simple algorithm that finds a classification rule. Start with the weights equal to zero. Now, do the following until you are bored: Grab an individual from the data set and see if your weights correctly predict the label from the attributes. If they don’t, update the weights by the rule
weights <-- weights + label*attributesThat’s it. You try out your classification rule, and if it doesn’t work on some example, you nudge the weights so they will be closer to correct when you try that example again. The perceptron is an example of negative reinforcement, where the prediction function is tested iteratively and only adjusted when it makes errors. As you might guess, positive reinforcement would be if we only made updates when we made correct predictions. We’ll talk about such algorithms in November.
It seems pretty intuitive that this little algorithm would find a rule that perfectly labels your data if you ran for long enough. If you keep seeing the same examples, and you know there is a perfect rule, the algorithm keeps pushing you in the direction of memorizing the dataset. But maybe you have doubts. Maybe you’re worried that this would take forever. Or that there’s some terrible organization of the data that causes some sort of cycling behavior that prevents the algorithm from ever converging on a good prediction.
It is surprisingly easy to prove that this is not the case. In 1962, Al Novikoff showed that no matter how you select examples from your data set, the perceptron algorithm makes a finite number of mistakes. Moreover, you can compute a bound on the number of errors. The bound uses two quantities.
Let D denote the maximum distance of an attribute vector to the origin in the population.
Let M(w) denote the minimum distance of an attribute vector to the decision boundary of the rule defined by w. Let M denote the maximum of M(w) over all separating rules, w.
These two quantities capture something about the geometry of the data when we conceptualize the attribute vectors as elements in a high-dimensional Euclidean space. D is giving us a measure of the scale of the data. M is giving us a measure of how separable the data is. Each decision rule splits the space of vectors into two regions: one where it’s positive and one where it’s negative. M is large when the data is very far from the region where the positive and negative halves meet. It is called the margin of the data set and measures how much wiggle room we have between positive and negative examples.
Novikoff showed the perceptron is guaranteed to mislabel at most D2/M2 examples. We provide his short proof in Chapter 3 of Patterns, Predictions, and Actions. No matter how many examples you have or how many attributes you use, this ratio determines an upper bound on its errors. It says that the further the positive examples are away from the negative examples, the faster the perceptron will find a perfect classification rule.
Maybe even more surprisingly (and certainly far less well known), we can explore how the perceptron performs on data we haven’t seen. Let’s now say your data is a subset of a larger population. You train the perceptron algorithm on a set of size K, and run it until it stops making mistakes. How many mistakes does it make on the N-K examples in the population that you haven’t seen yet? An astounding fact, proven in a book by Vapnik and Chervonenkis in 1974 but probably known much earlier, is that if the training set is sampled uniformly at random from the population, then the expected number of mistakes is bounded by
You can also find a proof of this result in PPA. The in-sample performance controls the number of mistakes out of sample. Moreover, the error rate approaches zero as the sample size increases. Provided you are getting something like a uniformly random sample of the sort of data you’ll ever want to predict,2 the perceptron finds an excellent prediction function.
The perceptron is a crown jewel of machine learning. It combines practical algorithms with insightful theory with short and intuitive proofs. It is parameter-free and has trivial updates. And its probabilistic extrapolation bounds have perfect constants and need no “big-O” notation. Nothing else checks all of these boxes.
Longtime argmin readers know I’ve grown increasingly skeptical of all theory about machine learning. But it’s seldom that we can’t learn something from applied mathematical models with such simply stated assumptions, simply implemented algorithms, and simply proven theorems.
And even if we want to quibble about the linear separability assumptions, almost everything that works in machine learning works by iteratively reducing errors on a training set of data using negative reinforcement updates that are reminiscent of the perceptron learning rule. There’s something deep here, even if the perceptron is shallow learning.
The biggest tension in binary classification is whether the negative class is labeled by 0 or by -1. It changes depending on the algorithmic context.
I know, I know, this is a huge and tenuous assumption.


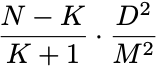
How does this differ from linear discriminant analysis, estimated by (say) maximum likelihood? Presumably the standard results show that it will converge to the correct model with enough data.