Probability Is Only A Game
Ruthless subjective probability without Bayes' Rule
Earlier this year, I spent a few posts discussing de Finetti’s “score coherence” as a motivation for probability. To review, if a forecaster is scored by a proper scoring rule, then their predictions must obey the axioms of probability. If they don’t, there is always a set of forecasts they could have provided that would get a better score.
Defensive Forecasting has a similar flavor. You can think of the forecasts as probabilities, and the forecaster chooses them so that no matter what the outcomes are, the errors obey the law of large numbers. Indeed, that’s a simple way to motivate the “game theoretic” strategy of Defensive Forecasting. Choose a forecast so that the error looks uncorrelated with the past, no matter what the future brings. This is precisely how Vovk motivates his K29* algorithm for calibration, an algorithm we discuss in Section 8. Indeed, “K29” refers to Kolmogov’s 1929 proof of the weak law of large numbers.
Another way to think about this is that the forecaster is choosing probabilities of future events so that it appears as though the future outcomes were generated as samples from those probabilities. That is, regardless of the outcome, any inquisitive statistician could be convinced that the outcomes were sampled from the forecasts. That you can do this at all is amazing. It also gives a new way to think about probabilities of one-off events.
Indeed, this connects Defensive Forecasting to the theory of outcome indistinguishability, a recent theoretical framework developed to grapple with the concept of individual risk. Outcome indistinguishability operationalizes the notion of individual risk. If you are in a sequential forecasting game, Defensive Forecasting generates real numbers that you can treat as probabilities of single future events. Forecasts are themselves the probabilities. They are “subjective” as they belong to the forecaster, but they are also “objective” as they are determined by an optimization problem. Notably, this optimization problem does not reproduce Bayes' Rule. Changing the evaluation function changes the update rule.
The “subjective part” here is what you are comparing to. In a game-theoretic setting, you construct a strategy so that you are (approximately) better than any player who saw the outcome in advance with the same computational toolkit. What goes into that toolkit—which data streams, which code libraries, which variables in OLS equations, which LLMs—is up to the forecaster.
What does the probability of an event mean? It’s what I forecast so that no matter what nature does, I do as best as possible in the forecasting game. The stakes of the forecasting game can be high! In Section 5 of our paper, we discuss the problem of sequential decision making, where the forecaster translates predictions into actions. Defensive Forecasting can produce competitive actions from competitive forecasts.
Defensive Forecasting and de Finetti’s score-coherent Forecasting are “Ruthlessly Bayesian,” if you will. The forecaster doesn’t pick probabilities to avoid being Dutch Booked, but rather picks probabilities to be the Dutch Book. The defensive forecaster is playing to win, and probabilities turn out to be optimal moves in the game. Notably, there’s no inference happening nor needed in this framing. This is a philosophy of probability based only in prediction and error correction.
I’m not saying I endorse this view of probability, but I think it’s an illuminating one. As so much of contemporary forecasting has turned into competition, there’s a lot of alpha in recognizing probabilities are moves in a game. You know, Vovk and Shafer wrote an entire book from this perspective. Two in fact! And indeed Bayes’ Rule appears nowhere in this book. Coherence and game-theoretic forecasting don’t need inference. I think that’s super interesting!
The ruthlessly pragmatic statistics of defensive forecasting and the bureaucratic statistics of regulation both don’t use probability as a mechanism of inference. This is fascinating to me. I tend to side with Meehl on this one: there is no universal mechanical rule to turn data into inferences. I remain willing to be convinced otherwise, but it’s interesting to see how probability can be invaluable in applied contexts even after you remove inference from the story altogether.
Let me close today by showing how outcome indistinguishability also gives mathematical insights into why Defensive Forecasting is effective. I left the equations for the very end today, so folks who don’t want this sort of thing can just say goodbye until tomorrow. But for those who want another high-level motivation for the Defensive Forecasting mindset, continue on!
Let’s assume that we make forecasts ft of outcomes ot so that the equations I wrote yesterday are satisfied.
Since the outcomes only take values of 0 and 1, the Brier score can be written in an alternative way:
This second expression is affine in the outcome. Using the Defensive Forecasting equations above, we can thus substitute forecasts anywhere we see an outcome:
That is, if we run Defensive Forecasting, we can assume that, in expectation, the outcomes and forecasts are equal. Similarly, for any constant prediction b, the same identities imply
Since the Brier Score is a proper scoring rule, we always have
That is, since we can assume our forecasts and outcomes are “equal” on average, we can conclude that our forecasts produce a lower score than any constant forecast. Even one that sees all of the outcomes in advance.
This reasoning can be applied quite generally. If you can assume your outcomes are sampled from your forecasts, then you can treat the forecasts as if they were probabilities and do all sorts of optimization analyses as if they were true. This provides a framework for generating probabilities and then sequentially solving “stochastic” optimization problems with these probabilities. It is the optimization framework itself that makes the probabilities useful, even if someone else thinks the probabilities are wrong.


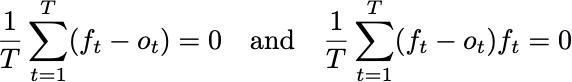
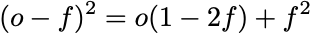
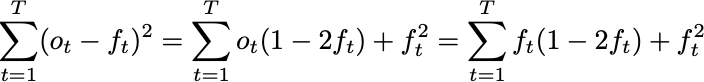
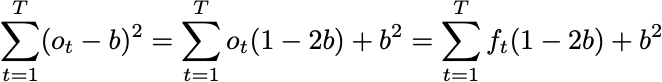
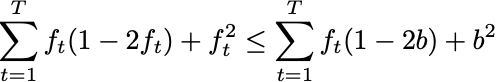
In a quant trading environment, framing decisions as stochastic optimization problems – even with imperfect probabilities - transforms forecasts into robust trading strategies. For us, robustness in parameter estimation was a primary focus, which in practice meant continually monitoring our models, especially wrt regime shifts & changing mkt conditions). But as I noted in comments to the site a few months ago, the joint hypothesis problem (#fama) always comes into play – tests of risk-adjusted outperformance rely on explicit pricing models, but the true mkt equilibrium model is unobservable.
Ultimately, this approach (treating forecasts as probabilities and embedding them in an optimization framework) is what makes the methodology both practical and powerful, even when the probabilities aren’t perfect. While realized P&L is the ultimate judge, it’s an incomplete measure because it doesn’t capture the opportunity costs, especially those arising from misspecified parameter choices or errors. And evaluating opportunity costs in a trading world where there is no time “T” is #ReallyHard.
Then again, applying a demanding degree of specificity to the problem of model formulation, estimation, and ultimately optimized decisions for live markets is a fool’s errand (unless you’re Jim Simon 😊). In practice, we fell back on the Herb Simon concept of “satisficing” rather than optimizing.