Restatements or Forecasts?
A slightly more sophisticated example of Defensive Forecasting.
Lots of folks in the comments were unimpressed with the example I used yesterday to defend Defensive Forecasting. Matt Hoffman wrote, “We care about a forecaster's average error, not the error of their average prediction.” John Quiggin quipped, “This isn't what I would call forecasting, but estimation.” I agree with both of them! What’s fascinating about Defensive Forecasting is that it lets you turn estimates into forecasts. If you can make predictions whose average has low error, you can also make predictions with low average error.
First, a bit of a defense of my defense (of Defensive Forecasting). I have been writing equationless posts as often as I can. Partially this has been as a writing exercise for myself to see how much I can explain before jumping into the Emoji & Symbols picker. Partially, it’s for you all, as if I can describe things well without mathematics, more people might be willing to read it. But I’m still at the point where I don’t know how to appease the folks in yesterday’s comment section without a few equation displays.
Let’s dive in then with what I hope is the most accessible example of something John Quiggin might call forecasting. Ryan Tibshirani came up with the following argument, and Juanky and I couldn’t figure out how to fit it into the paper. So let me share it with you all on the blog.
The defensive forecasting game goes in turns. The forecaster sees the current state of the world and makes a prediction. They then observe an outcome and are incrementally scored. The game repeats.
Let’s leave the state of the world in this first example. You can perhaps see from today’s argument how you might add it in.1 The forecaster is just predicting yes/no without any additional context. The free-throw example from yesterday works here. We want to predict whether the same basketball player will make their next shot without deeply considering the context in which they are shooting. Let’s use the Brier Score to measure our performance.
To define the Brier Score, I’ll use symbols. Let ft denote the forecast at time t. This is a real-valued number, such as 0.72. We can represent the outcome at time t with a variable ot, equal to one if the event occurs and zero if it doesn’t. Then the Brier Score is the sum of the squared errors:
What would it mean for our forecasts to be good? If we’re not allowed to use any information about the player or context in this simple setup of the forecast game, perhaps the best we could do is try to beat a constant prediction. We’d like to construct a stream of forecasts so that for any boring constant forecast, b,
Now, if I have any quantitative social scientists still reading the blog, you’ll see that this looks like an optimality question for least squares. I’m asking that for all real numbers a and b, the minimum value of
Occurs when a=1 and b=0. How can we guarantee that this is the case? We can look at the optimality conditions for least squares. We need
You can derive these conditions by taking derivatives with respect to the parameters a and b. The first condition here is exactly saying that we want the forecaster’s average prediction to have zero error. This was what I showed how to do with Defensive Forecasting yesterday. The second term is similarly a property of the average prediction.
What we can conclude so far is that for appropriately chosen quantities, having predictions that have averages with low error implies that your predictions have low average error. Unfortunately, I don’t know how to guarantee that our predictions will satisfy these optimality conditions exactly. Defensive Forecasting, fortunately, provides a method to satisfy these conditions approximately. And then, if you do a little more algebra, you can propagate your errors back to the original question and show that the resulting Brier Score is competitive with the best constant prediction. Read the paper for the details!2
Here’s how Defensive Forecasting makes both of these expressions small. When tasked with making a prediction of the future at time T, the forecaster chooses fT so that no matter what oT is, it looks like the forecasts are closer to satisfying the least-squares optimality conditions. If you write out the expression in norms, you see
There are three terms on the right-hand side of the equation. We’re stuck with the first term because it’s the error we’ve accumulated so far. Your forecast can only make the second two terms small. Now, whatever you predict, the third term is at most 2. We can simply accept whatever we receive from the third term and choose a forecast to ensure the second term is less than or equal to zero. If we could do this whenever we forecast, then the term on the left-hand side is bounded by 2T. This means the optimality conditions above will have magnitude at most (2/T)½ and are thus approximately satisfied.
The fun part is that it’s very easy to find predictions to make that second term less than or equal to zero. First, try forecasting fT=1. If the inner product in that second term is non-positive, then no matter what oT is, the second term is non-positive. If that doesn’t work, try fT=0. If the inner product is now non-negative, the expression will be non-positive no matter what oT is. If neither works, then there has to be a forecast fT that makes the inner product zero. You can predict that.
If you forecast this way, making predictions so that your next error looks “anticorrelated” with your past predictions, you are guaranteed to produce a sequence of forecasts that converge to the desired optimality conditions and hence have a competitive Brier Score.
I am not arguing that this is the best algorithm we could have used. There are lots of ways to get a small Brier Score that are not necessarily Defensive Forecasting. The best algorithm I know for this simple problem is forecasting the running average of the events that have happened thus far. I don’t have a clean way to yet show that the running average is defensive forecasting in the narrow definition we use in our paper. However, it’s clear that the running average is only a function of what you’ve seen before. That it has something to do with the future is our leap of faith.
Or you could check out Section 6.
And hat tip to Matt Hoffman for finding the typo in the display right after equation 3. There should be a T2, not T, in the denominator.


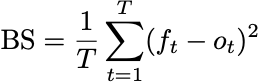
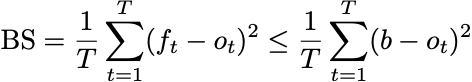
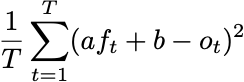
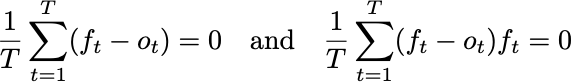
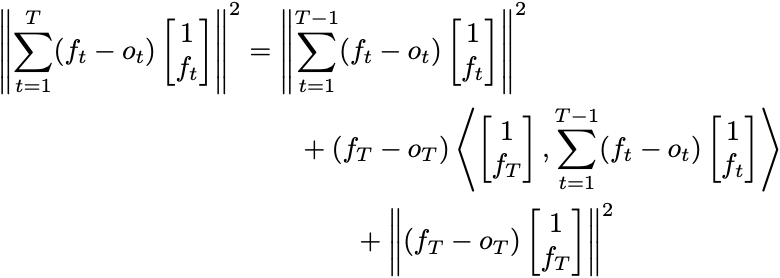
I just wanna say I really appreciate the fact that you take the effort to turn all the complex math into simple mathematics that mathematically illiterate idiots like me can understand.
Thank you for this write-up! I'm currently reading the paper, and it wasn't immediately clear to me what role anti-correlation search was supposed to be playing. This exposition made it very clear.