Looking above and below
I've finally found a satisfying derivation of Lagrangian duality.
This is the second part of the live blog of Lecture 9 of my graduate class “Convex Optimization.” A Table of Contents is here.
What a difference a lecture makes. Yesterday morning, I was apprehensive about class because I couldn’t find a satisfying and intuitive explanation of duality. But… now I think I have one? Let me try it out on you, my dear readers, and let me know if this clarifies anything for you or if it makes things even more confusing.
Advance warning: I’ve been trying to keep these blogs on the less technical side, but Friday posts have ended up being extra technical. Today’s Friday post is not an exception to this emergent rule.
Earlier this week, I discussed what it would mean to prove that you’ve found a solution to an optimization problem. If you have a candidate solution, you can plug it in and check feasibility. This is usually easy enough to compute. However, verifying optimality was more involved as we had to check conditions held for all points in the feasible set. I gave a few examples of ways to construct such proofs of optimality. Duality theory provides a path that generalizes all of them.
The main idea is to construct lower bounds. If you had a way of rigorously generating lower bounds on the optimization problem, and the lower bound equaled the objective value of your candidate solution, then you would have a proof of optimality. You need a potential solution and a lower bound saying that all points have objective value greater than or equal to the one you are proposing.
Duality starts with an explicit construction of lower bounds to optimization problems. We find a family of lower bounds and then construct a dual problem by finding the best lower bound. This will be called the dual problem.
Let’s consider the constrained optimization problem.
For now, I won’t assume anything about the convexity of these functions. We can think of constrained optimization as unconstrained optimization if we let ourselves work with functions that can map a point to infinity. Solving the optimization problem is the same as minimizing the unconstrained function
You might not have a good algorithm to deal with infinities, but from a conceptual standpoint, this extended real-valued function captures what the optimization problem means. The only x with finite objective are the feasible points.
I can define a family of lower bounds for my extended real-valued function p(x) by introducing the Lagrangian:
The Lagrangian has three arguments. It takes a primal value x and two Lagrange multipliers 𝜶 and β. For fixed Lagrange multipliers, the Lagrangian is a lower bound of the function p as long as 𝜶 is greater than or equal to zero. This is because if you plug in a feasible x, the first summation will be nonpositive and the second summation will be zero. Therefore, the Lagrangian yields a value less than f0(x). For a nonfeasible x, the Lagrangian will be some number less than infinity.
How tight are these lower bounds? For a fixed x, we have
That is, for each x, there is a sequence of Lagrange multipliers so that the value Lagrangian converges to p(x). To see why, note that if x is feasible, you’re going to want to set 𝜶i to zero whenever an inequality constraint is satisfied. But if x is not feasible, the supremum must be infinite. If fi(x) is greater than 0, the supremum of 𝜶i is infinity. Similarly, if an hj(x) is nonzero, the supremum with respect to βj is infinite. Following this argument to its logical end, I’ve argued that the original optimization problem we cared about is equivalent to the minimax problem
Now let’s think about the quality of the lower bound provided by each fixed assignment of the Lagrange multipliers. First, the Lagrangian is unconstrained, so you might try to run gradient descent to find a minimum. Since this Lagrangian function is a lower bound of our optimization problem, if the minimum that you find is feasible, you have found an optimal solution of the optimization problem. That’s pretty powerful already! If you instead find a nonfeasible point when minimizing the Lagrangian, you still get a lower bound on the optimal value of the original optimization problem. For each 𝜶 and β, we can quantify the value of this bound with the dual function
The value of g is always a lower bound on the optimal value of the optimization problem. Over all choices of the Lagrange multipliers, the best lower bound is also a lower bound. The maximin problem
is called the Lagrangian dual problem or usually just the dual problem. Our original problem is then retroactively dubbed the primal problem. The optimal value of the dual problem is always a lower bound of the primal problem. This inequality is called weak duality and follows from the simple argument I wrote yesterday. Today’s exposition has motivated duality as a way of generating lower bounds, so this shouldn’t be too surprising.
Now, why should we care about this family of lower bounds? The Lagrangian is an affine function of the Lagrange multipliers. The dual function is an infimum of affine functions. That means it is concave, no matter what fi and hj are. The dual problem is always a convex optimization problem.1 We’ve derived a powerful tool to construct lower bounds for intractable problems.
In convex programming, there’s a second remarkable benefit. If the primal problem is convex and properly conditioned, then the dual and primal optimal values are equal. This is called strong duality. With strong duality, we have arrived at our initial goal of proving a particular solution of the primal problem is optimal. A dual optimal solution certifies the optimality of a primal optimal solution. Moreover, these primal and dual solutions often come in pairs, where you can compute one from the other. I will cover strong duality and such optimality conditions next week.
I hate the terminology, but we’re stuck with it: maximizing a concave function over a convex set is technically a convex optimization problem



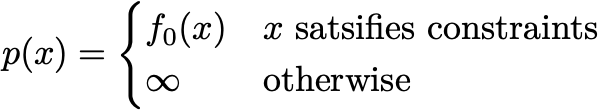





I really liked this lecture! I first saw Lagrangians in 227A and didn't really understand them, but I think this is helping me start to get there...
"Therefore, the Lagrangian yields a value less than f_0(x)." Did you mean p(x)?