Desirable Sins

Robustness of the holdout method and paths forward for machine learning theory.

This is a live blog of Lecture 14 of the 2025 edition of my graduate machine learning class “Patterns, Predictions, and Actions.” A Table of Contents is here.

Ed Leamer, one of my favorite late 20th century critics of statistical methodology in the social sciences, posed a colorful metaphor about the gap between theory and practice in his 1978 book Specification Searches. He observed a striking disconnect between the rigid rules of econometric theory and the actual analysis done by those who had to grapple with reality.

“We comfortably divide ourselves into a celibate priesthood of statistical theorists, on the one hand, and a legion of inveterate sinner-data analysts, on the other. The priests are empowered to draw up lists of sins and are revered for the special talents they display. Sinners are not expected to avoid sins; they need only confess their errors openly.”

The hierarchy manifested itself in the office layout of the economics department, with the applied folks stuck in the basement, and the theorists comfortably seated on the third floor.

“...the econometric modeling was done in the basement of the building and the econometric theory courses were taught on the top floor (the third). I was perplexed by the fact that the same language was used in both places. Even more amazing was the transmogrification of particular individuals who wantonly sinned in the basement and metamorphosed into the highest of high priests as they ascended to the third floor.”

This disconnect perfectly describes machine learning in the early 21st century. We had a set of lofty rules that we pieced together from statistics, functional analysis, and optimization theory. These suggested a way forward for rigorous predictive engineering practice. But practical progress was made by sinning in the basement: Ignoring bias variance tradeoffs, building high-capacity models, using nonconvex optimization, and training on the test set.

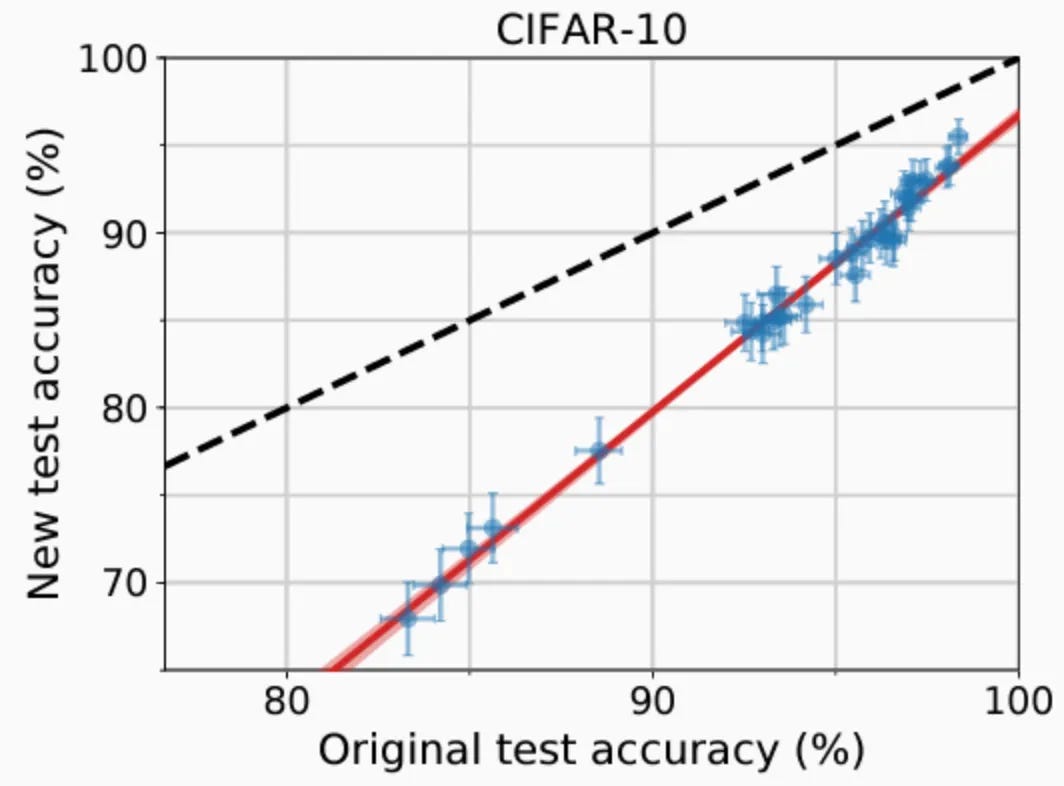
Machine learning theory needs a reformation, because our advice is not just ignored, but demonstrably, actively harmful. My theses for this reformation are based on the work my collaborators and I have done over the last decade. I’ll discuss this graph again, which completely changed the way I think about machine learning.

For folks who are new to argmin.net, this chart plots a replication experiment in machine learning. We generated a new test set for a benchmark called CIFAR10. Using the instructions specified by the authors, we attempted to sample data identically distributed to the original test set. We then downloaded a bunch of trained models and compared their performance on the original test set (x-axis) to our new set (y-axis). We found that models that performed better on the old test set, those explicitly trained on a stale test set, also performed better on the new test set. The ordering implied by the test-set leaderboard was preserved under replication. Training on the test set was virtuous after all. However, all models suffered a performance drop on the new test set. Machine learning models could be surprisingly fragile to seemingly small changes in the data-generating process.

We’ve since reproduced this phenomenon in hundreds of other data sets. Empirically, the associated phenomena have been staring us in the face since the beginning of machine learning. But sometimes it just takes one set of experiments to reorient our thoughts.

• Training on the test set does not lead to overfitting.

• Iid data is a convenient model, but small perturbations to the assumption lead to significant performance drops.

• Machine learning does not have a replication crisis, but it might have an external validity crisis.

• Most of the practice we teach as gospel is mythology.

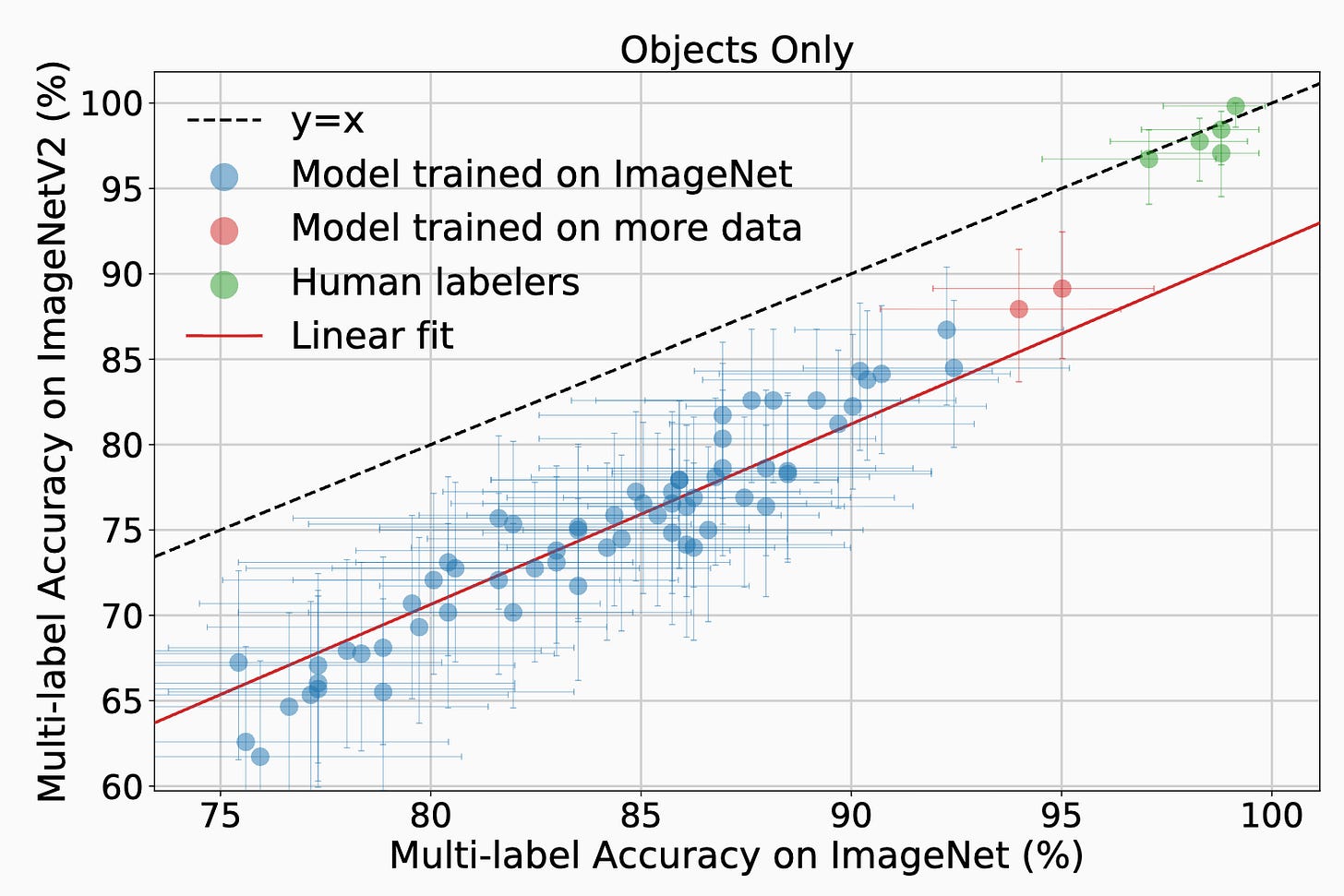
Maybe one of the less appreciated implications of this family of plots is that you shouldn’t train on the training set. Here’s another plot that’s on a larger data set with more models.

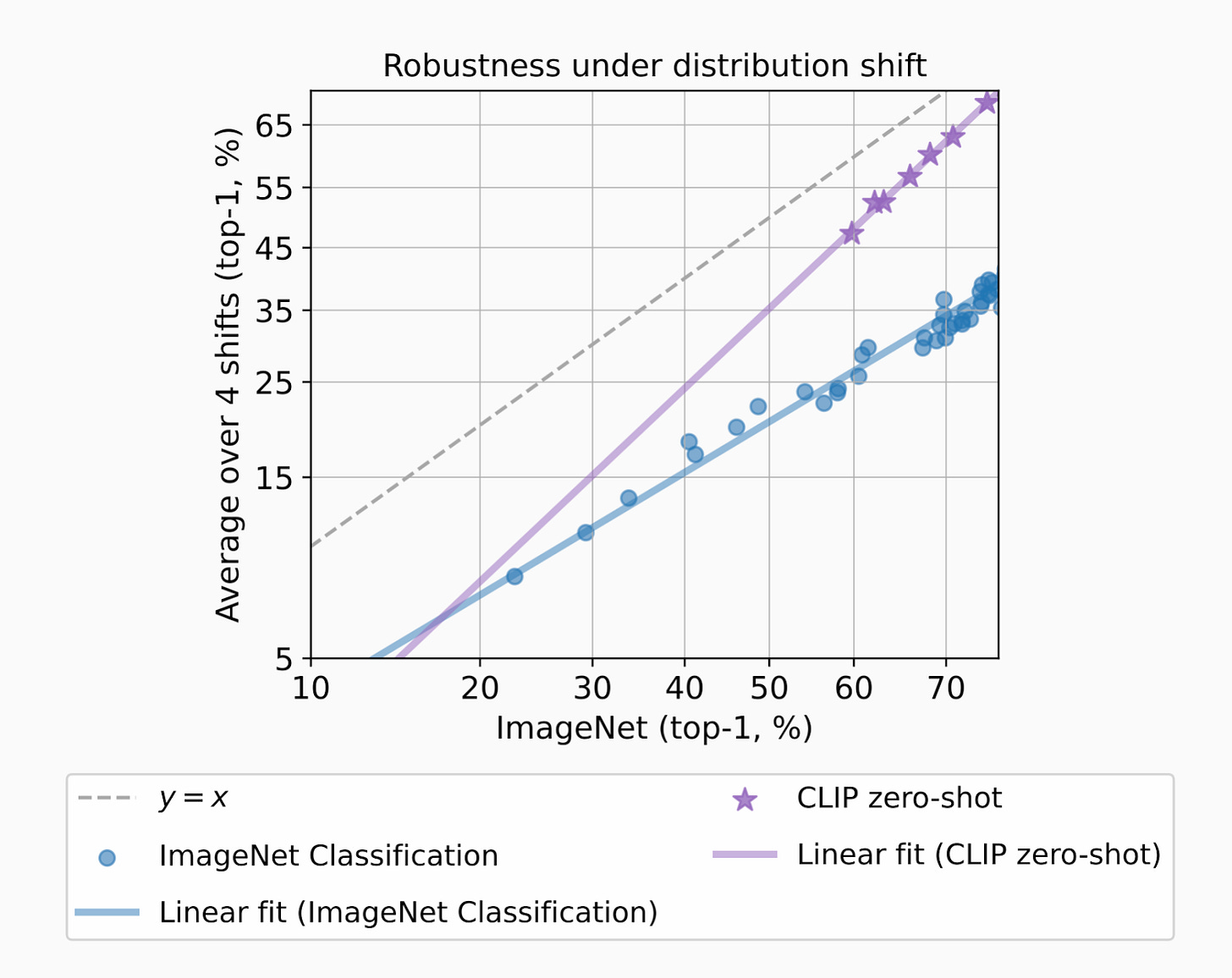
In this work, some of my graduate students and post-docs trained themselves to identify images in ImageNet. They are the five dots at the top of the page. The drop in performance on new test sets is an artifact of supervised learning, not the content of the test examples. Since then, people have found clever ways to move closer to the ideal dashed curve by pretraining on data that is completely unrelated to the ImageNet task. A great example is OpenAI’s closed data model CLIP, which solidly gets off the line of models trained on ImageNet.

OpenAI trained CLIP by building embeddings that correlated images with the text accompanying them on the internet. The data set was somewhere in the range of 400M images. They then evaluated ImageNet performance by inputting all of the possible labels for an image and seeing which text embeddings were most aligned with the image embedding.

Someone should come up with a more general way to do this! Understanding how to scalably capture this phenomenon, where “pretraining” (whatever that means) provides robustness against overfitting to a supervised learning task specification, can help us walk down the path to more scalable, efficient, open generative models.

Unfortunately, I don’t have a specific mathematical guide for how to move forward. All of my recent machine learning theorizing has been sociological, historical, or philosophical. I can’t give you a formula for how large your test set should be. I can’t give you a formula for what makes a compelling benchmark or when you should build a new one. I can’t give you a precise way to efficiently avoid training on the training set. But I’m thinking about it! And my main point in repeating this lecture is that I hope the theoretically minded readers out there will think about it too.

We can take inspiration from Leamer’s book, which is not just skeptical. It strikes an important, optimistic chord.

“In this book I discard the elitism of the statistical priesthood and proceed under the assumption that unavoided sins cannot be sins at all. For several years I have observed colleagues who analyze data. I report herein my understanding of what it is they are doing. The language I use to describe their behavior is the language of the statistical priesthood, and this book may serve partially to bridge the gap between the priests and the sinners. The principal outcome of this effort is an appreciation of why certain sins are unavoidable, even desirable. A new sin does emerge, however. It is a sin not to know why you are sinning. Pointless sin must be avoided.”

Here are some other related blog posts and papers if you want to follow up.

Papers:

• “Do ImageNet Classifiers Generalize to ImageNet?” B. Recht, R. Roelofs, L. Schmidt, and V. Shankar. ICML 2019.

• “A Meta Analysis of Overfitting in Machine Learning.” R. Roelofs, S. Fridovich-Keil, J. Miller, M. Hardt, B. Recht, and L. Schmidt. NeurIPS 2019.

• “Cold Case: the Lost MNIST Digits.” C. Yadav and L. Bottou. NeurIPS 2019.

• “Evaluating Machine Accuracy on ImageNet.” V. Shankar, R. Roelofs, H. Mania, A. Fang, B. Recht, and L. Schmidt. ICML 2020.

• “The Effect of Natural Distribution Shift on Question Answering Models.” J. Miller, K. Krauth, B. Recht, and L. Schmidt. ICML 2020.

• “Measuring Robustness to Natural Distribution Shifts in Image Classification.” R. Taori, A. Dave, V. Shankar, N. Carlini, B. Recht, and L. Schmidt. NeurIPS 2020.

• “Do Image Classifiers Generalize Across Time?” V. Shankar, A. Dave, R. Roelofs, D. Ramanan, B. Recht, and L. Schmidt. ICCV 2021.

• “Data Determines Distributional Robustness in Contrastive Language Image Pre-training (CLIP).” A. Fang, G. Ilharco, M. Wortsman, Y. Wan, V. Shankar, A. Dave, L. Schmidt. ICML 2022.

Blogs:

• You got a 9 to 5, so I’ll take the night shift

• Holding out for an explanation

• The Adaptivity Paradox

• In Defense of Typing Monkeys