The Adaptivity Paradox
Test-set reuse: the problem that wasn't.
It’s easy to cook up theory to convince yourself that all machine learning practice is overfitting. Statistical dogma states that every time you look at a holdout set, you leak information, defiling its purity. Let’s unwrap how this could be a problem.
For any prediction function f, we’d like to understand how it will fare on data in the wild. Define the external error, errext[f] to be the error rate of the function on data we’ll evaluate in the future. Define the internal error, errint[f] to be the error we see on the data we have collected so far.1 Finally, let’s say we take some of our data, put it in a special box, and call it a “testing set.” The test error, errtest[f], is the error observed on this test set.
We can estimate the external error using the following decomposition.2
We hope that our set selection data makes the difference between the internal and external errors small. We hope that good data hygiene means that the test error is a reasonable estimate of the error on the data we’ve collected. And hence, we hope that the error on the test set is a reasonable signifier of the external error.
There is some reasonably attractive theory that gives us some intuition about how to select and use a test set. If you sample the test set uniformly from your data set, a single prediction function will satisfy
You can derive this bound using Hoeffding’s inequality. It’s a gross overestimate of what you see in practice, but it suggests that larger test sets will provide better estimates of the internal error. This analysis also suggests that the test set size need not grow as a function of the dataset size.
If you line up a family of K candidate prediction functions in advance and test them on the test set, you can apply a union bound argument to get that
for all K of the prediction functions. This analysis, which is again woefully loose, says that if you want to test a lot of functions, it’s OK because your test sample only needs to grow logarithmically with the number of possible functions. The logarithm of 10,000 is about 9, and the logarithm of a trillion is about 27. For a factor of 3, you get a huge number of extra queries. Importantly, you don’t need a trillion test samples. For machine learning, something in the thousands seems reasonable.
Standard theory suggests we can reuse the test set a lot! But there’s a caveat. For this analysis to work, I must list my candidate prediction functions in advance. If I am allowed to look at the test set and then pick an f with the error I see, I can do something devious.
Let’s suppose that we are working on a simple binary classification problem where there are exactly two possible labels for each data point. For convenience, let’s let the choices be +1 and -1.
Let me define a class of n+1 prediction functions as follows. For the first n of them, I’ll choose random functions, predicting a random label for each data point. The test error on these predictions will be approximately ½. The internal errors will also be about ½. But they won’t be exactly ½ because random fluctuations will induce variance.
I now record the test errors for the n random predictions. Without looking at any of the data, I can then find a linear combination of these functions where the test error is zero, but the internal error remains at ½. Why? It’s because the test error is a linear function of the test labels:
From the set of n test errors, I can solve this system of equations to find the labels on the test set.
OK, so what broke here? How did I get such a large gap between the internal and test errors? This is a problem of adaptivity. I used previous queries to influence a following query. In doing so, I broke the promises I made in my earlier statistical reasoning.
With adaptivity, you can get strikingly small test error with far fewer than n queries. Each query reveals something about the test labels. What errors can you get with K queries? A decade ago, Moritz Hardt proposed a simple boosting strategy. If you take only the T queries that get test error at least ½-s, majority voting gets you a classifier with test error no worse than exp(- 2 s^2 T).3 Straightforward analysis shows that approaches like this can get you an error rate of
The log K has become a K. Yikes. This seems bad!
We’re not as malicious as this in practice, but surely our leaderboard climbing and SOTA chasing are leaking something about the test sets. What happens when you tune hyperparameters by looking at the test error? The popular tuning methods use quote-unquote “reinforcement learning,” which, for the layperson, is trying a bunch of random things and then taking mixtures of what worked well. I’m sorry, but modern reinforcement learning is Hardt’s Boosting attack. Shouldn’t your excessive tuning cause so much test set leakage that you get overly optimistic about your external performance?
The answer seems to be no. And I have no idea why the answer is no. If you use the test error to select among functions that interpolate the training set, you seem to get very good prediction functions. Models continue to improve on external data after a decade or more of test set abuse. When we looked at Kaggle competitions, the public test leaderboard errors were perfect predictors of the private test errors.
So why? This is a great theory question! I mean, we shouldn’t let rigor get in the way of a good time, but shouldn’t we care about why this method of competitive testing and frictionless reproducibility seems to work despite its apparent flaws? Is the intuition from Hoeffding’s inequality just wrong? Is statistical deduction simply invalid?
I have no good answers, but I’d love to hear yours.
In machine learning theory, these are more commonly called the population risk, the empirical risk, respectively.
Yes, this sort of thing is the start of many the machine learning theory paper. Add and subtract the same quantities and declare derived insight.
This follows from Hoeffding’s Inequality again! It’s as if learning theorists only have one tool.






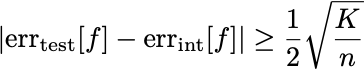

I think your err_ext decomposition has some sign errors?
"It works in practice but not in theory."
But seriously though, I think the intuition from coin flips is misleading because 1d space still has a reasonable Euclidean metric but in the real world use cases (or anything above 9d) you don't want Euclidean but Manhattan metric. It gets even harder (for me at least) to have intuition about how nonlinearities impact a space and the metrics defining how far apart thing are. Basically I think it works because with enough parameters you can make points sufficiently, though probably not arbitrarily, far apart.