Twirling Towards Freedom
Avoiding dynamic programming with dynamic programming
This is the live blog of Lecture 23 of my graduate class “Convex Optimization.” A Table of Contents is here.
Since we’re in the middle of an endless AI bubble, most people encounter control theory in the context of reinforcement learning. RL classes and tutorials present “classical control” as the problem of finding solutions to Markov decision problems. They consequently sell Dynamic programming as the solution to all control problems. From dynamic programming, a variety of RL methods can be derived, whether they be Q-learning, policy gradient, or whatever the kids are into these days. I’ve lost track of what is trendy in the fog of foundation models. I just know that people insist it’s still worth throwing a ton of money at these sorts of things.
The issue with dynamic programming is that it is much less applicable than it seems. Dynamic programming works great for LQR, and it’s ok for small Markov Decision Processes. Unfortunately, the problem becomes intractable once you move away from these two special cases, and we get mired in a mess of approximation methods.
From our modern optimization perspective, it’s worth emphasizing two approaches that completely obviate the need for dynamic programming. The first is batch solvers. For most reasonable convex control problems, including finite time horizon MDPs and LQR, cvxpy can nearly instantaneously find you the optimal solution. This is an application where optimization software shines. And yeah, this is why SpaceX can use model predictive control to land rockets. Even more amazingly, such solvers enable small embedded insulin pumps to run MPC to manage type I diabetes. Batch solvers are perfectly suitable for a multitude of applications, letting the designer spend more time on modeling dynamics, uncertainty, and robustness and less time worrying about how to solve optimization problems.
The second approach uses fast recursion, leaning on ideas from filtering.1 This method was popular in the 1960s for trajectory optimization and is inspired by Pontryiagan’s “maximum principle’ approach to optimal control. The idea is to use duality to guide your algorithm design. And the algorithm that comes out is more successful than any proposed approximate dynamic programming RL method.
Today, I’ll show you three applications of the same idea. Let’s start with the classic Linear Quadratic Regulator problem:
Here, we have convex quadratic costs and linear dynamics. This problem famously has a “closed form” dynamic programming solution that involves Riccati equations. However, we can derive this solution without appealing to value functions and costs-to go. I’ll instead just use convex duality. Introducing a Lagrange multiplier 𝝀t+1 for each constraint, the KKT conditions for this problem are
The first equation tells us that the Lagrange multiplier fully determines the control signal at time t at time t+1. Hence, we only need to solve the second two equations, which relate the dynamics of the state to the dynamics of the Lagrange multiplier. We thus call the Lagrange multiplier the costate. The costate obeys adjoint dynamics that run backward in time. This motivates a solution to the problem: solve for the costate in terms of the state by running backward in time, then solve for the control signal by running the dynamics forward in time. As Stephen Boyd demonstrates in his lecture notes, this recursive algorithm recovers the LQR solution.
The LQR problem admits a closed form solution because of its quadratic costs. For non-quadratic objectives, we can’t hope to solve the KKT conditions exactly. Instead, we have to rely on iterative algorithms. Boyd and Vandenberghe show that even for non-quadratic optimal control of linear systems, the KKT system associated with the Netwon step is banded. Hence, the Cholesky factorization admits a recursive solution that runs in time scaling linearly with the time horizon. A smart solver will take advantage of this automatically.
Additionally, the adjoint method using Lagrange multipliers can be applied to compute a gradient step. Let’s suppose we want to solve the optimal control problem
Where J is a nonlinear cost:
This problem has convex, non-quadratic costs and time-varying dynamics. To run gradient descent, we can approximate the cost function using a first-order Taylor expansion. Fix a starting pair of controls and states (ut(0), xt(0)). This yields the approximation
This approximate cost is a quadratic function. Hence, we can minimize the approximation subject to the dynamics constraints. Again, using a Lagrange multiplier 𝝀t+1 for each constraint, the KKT conditions for minimizing the approximate cost are
These KKT conditions are even easier to solve than the LQR conditions. First, you compute xt(0) by running the dynamics forward with the control signal ut(0). Next, you compute the costates, running backwards in time. You might say you are propagating the gradient information about x backward. Finally, you can calculate the gradient step of the control signal by adding the gradient information computed from the costate.
This gradient method, called the method of adjoints, has very fast iterations. Each step requires only an order of T computations. It turns out to be generally applicable far beyond the realms of optimal control.
Let’s say you are an intrepid deep learning researcher. To find a new AGI model, you have derived a loss minimization problem of the form.
Here F is a function from features to labels. You propose a complex model with keen inductive bias writable as a giant composition:
Each function in this expression has a vector of parameters that you need to optimize for maximal agenticness. You come to my office hours asking for a good algorithm. I put on my optimization hat and suggest that you rewrite the unconstrained minimization problem as a constrained one:
With this transformation, you can apply the adjoint method and get a gradient step. If you write down all the equations, you’ll find this is just backpropagation.
If you want to see the details of how the method of adjoints is the same as backpropagation, check out this blog from 2016. It’s one of my favorites. You can also check out this follow up using the Implicit Function Theorem to show the Lagrange multiplier derivation remains correct for nonconvex problems.2 The KKT conditions are sufficient for local optimality even when the problems are nonconvex. In our age of LLMs, it’s good to remember that many of the foundational ideas have convex roots.
There’s an unfortunate namespace collision here. When I say dynamic programming, I mean Bellman’s approach to optimal control. When computer scientists say dynamic programming, they mean a recursive algorithm that maintains a memoization table. Today's algorithms are all examples of the latter but not the former!
All of my pre-substack blogs remain online at archives.argmin.net. I’ve scattered pointers to the archive on the substack.






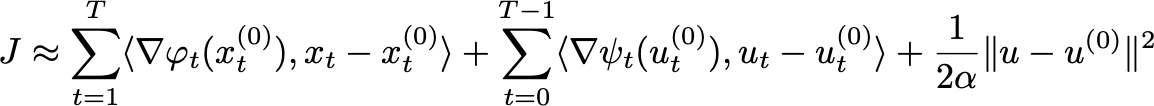
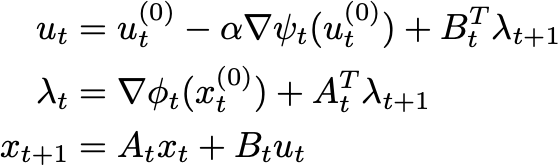
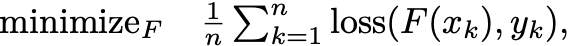


Those Boyd 2008-ish lecture notes are action-packed. Thanks for linking them.
This is so beautiful. I hadn't seen this before. Thank you!