Should you go for 2 down 8?

A battle of nerds against nerds over football analytics

On Sunday, the Tampa Bay Buccaneers made a last-ditch effort to topple the mighty Detroit Lions. Trailing by 14, they scored a touchdown with 5 minutes left to go in the game, bringing them to within 8. After the touchdown, they decided to go for a two-point conversion to make it a six-point game. The conversion failed, and the Bucs would eventually lose because Coach Todd Bowles forgot to use his final timeout.

After the failed two-point attempt, the insufferable Cris Collinsworth went on a longwinded explanation of why analytics say going for two down eight is always the right move. I tweeted that Cris Collinsworth lecturing the world on probability was my personal hell.

I almost blogged about this yesterday. The “go for 2 down 8” (G42D8) controversy is not only related to what I posted on Friday about Pro Football Focus but aligned with this blog’s insurgence against probabilistic reasoning. But then the world moved on to explain why Josh Allen is the new Philip Rivers, and I decided to work on blogs about the algorithmic intricacies of confidence intervals.

But I’m back today because Mina Kimes jumped into the fray. Kimes is the smartest person covering the NFL on ESPN. She’s probably the smartest person covering the NFL period. And though I doubt she’ll read this, she inspired me to write down why the G42D8 madness is flat-out wrong.

The G42D8 probability calculations out there on the internet are naive and don’t take into account all possibilities. They suggest G42D8 increases the probability of winning by over 12%, while more realistic calculations show the strategy increases the chances of winning by less than 1% (at best!). Even worse, the G42D8 calculations appeal to the inverse gambler’s fallacy, assuming that the probabilities of events do not change with time or context. But if you don’t assume that all events in football can be reduced to biased coin-flipping, then you can’t say much at all. You must understand the context before throwing a fade route in a vain attempt to go down by 6.

Let’s go through these points one by one. First, let me recap the argument for G42D8. This Reddit post explains the reasoning perfectly, and I’ll paraphrase the argument here. You first make some very strong assumptions:

• All 2-point conversions are equally likely to succeed.

• You will stop the other team from scoring.

• You will get a touchdown on the subsequent drive.

• The clock expires after that.

• There are even odds of winning in overtime.

Obviously, none of these are true. But go with it for now. To simplify things even more, let’s also assume that extra points are always made. Under this model, if you kick extra points after each touchdown, you go to overtime and win with a probability of 50%. 

What if you go for 2? Let P be the probability of making a two-point conversion. There are now two cases. In case 1, you make the 2-point conversion, kick the extra point, and win. In case 2, you miss the 2-point conversion and attempt another 2-point conversion on the next touchdown. The probability of your second 2-point attempt succeeding is again P. If you get the 2nd 2 pointer, you go to overtime and win with probability 50%. Combining these two possibilities, the probability of winning is

\(P + (1-P) \cdot P \cdot 0.5\)

If the odds of making a 2-point conversion are 50%, this calculation tells you that the probability of winning is now 62.5%. That’s much higher! Who wouldn’t take 1.7:1 odds over even odds?

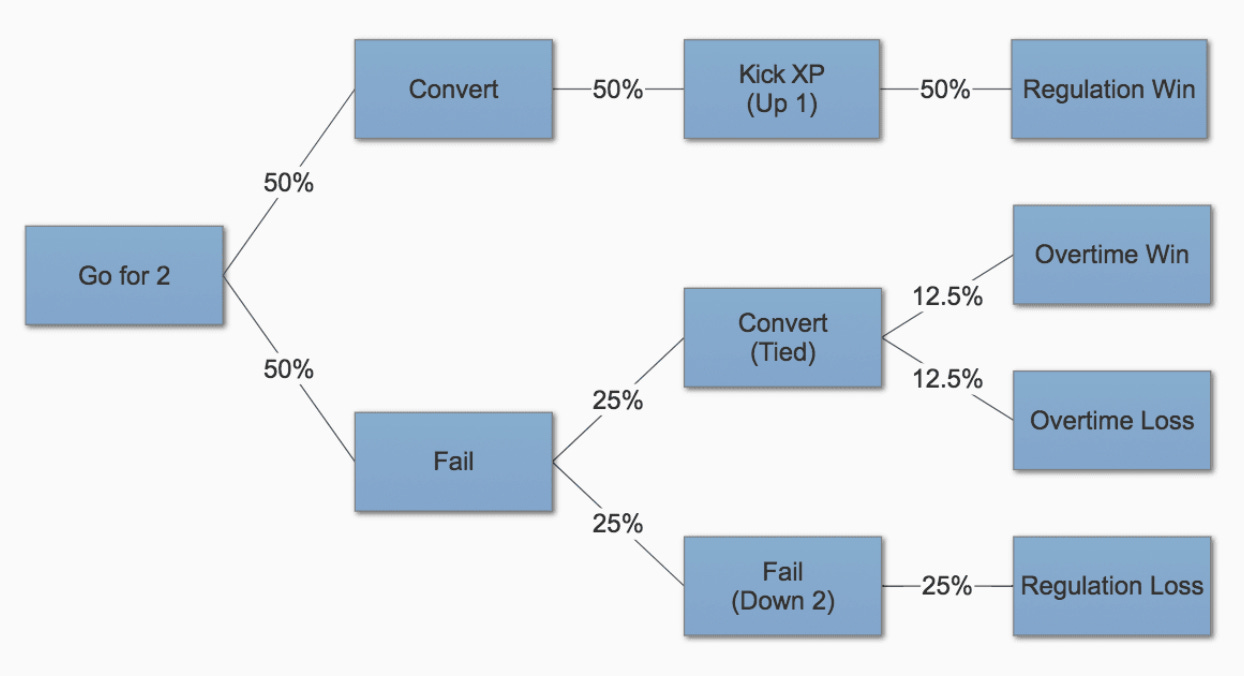
This flow chart made the rounds on Twitter after the game (originally from this post), graphically describing this strategy. It might be easier to digest than the analysis I wrote. YMMV.

There are multiple problems with this naive analysis. First, it does this weird thing where it assumes the probability that you stop the other team and score a touchdown is 1. What if you factored in the chances of stopping the other team and the chances of you then scoring a touchdown?

Punk Rock OR Star Laura Albert ran this much more realistic calculation in 2019. Math nerds should check this out, as it’s a great application of Dynamic Programming. Arrogant analytics people should check this out because it shows how complex exact probability calculations can be.

Laura is upfront with her assumptions. Notably, she states right out that she is assuming every drive is probabilistically independent of each other. The probability of scoring on any drive is constant throughout a game. It doesn’t depend on the score. The probabilities don’t depend on the time left. And they don’t depend on anything the teams actually do during the game. Anyone who has watched any football knows this isn’t true. But it’s a start for calculating stuff! So let’s press on.

Under these assumptions, Laura uses a computational technique called Dynamic Programming to evaluate all possible scenarios in the game tree. Once you factor in this more complex set of possibilities, the “62.5%” mirage disappears. Laura finds that if you are down by 2 TDs, G42D8 increases your probability of winning by less than 1%.

Less than 1%! That means G42D8 is by no means a clear bet at all. And all the bros on the internet comparing this to the Monty Hall problem and yelling about how “it’s elementary math” are telling on themselves. The full computations of the actual probabilities are hard! And if you add any degree of realism, the story is not cut and dry at all. Under completely unrealistic assumptions, G42D8 improves the chances of winning by less 1%. If there is any uncertainty in these calculations at all, then you might even be putting yourself at a disadvantage!

This brings me to my final point. Even Laura’s calculation assumes that each sequential event in football is independent of everything that’s happened before. Anyone who has watched any football knows this isn’t true. If this were true, teams would go for two every time. Teams would never try to make half-time adjustments. Teams would never use trick plays.

There are undeniable psychological and physical factors that shift the likelihoods of outcomes in football games. There are different stadiums and weather conditions. Defenses can get winded if they’re on the field too long. Even a tiny hamstring tweak can change the explosiveness of a receiver. The hot hand is real. 

And, I’m sorry, but momentum exists. Sure, the way football heads talk about momentum shows they don’t mean the same thing as how it’s defined in classical physics. But that doesn’t mean the concept doesn’t exist. Part of football is intimidation and getting the other team to mentally beat itself. I concede that teams’ mental states can change at the drop of the hat with a foolish fake punt or a fumble out of the back of the endzone. But that doesn’t mean their states of confidence and aggression aren’t real.

In fact, I’d argue that the G42D8 strategy can work as a mind game! In December, Mike Vrabel figured the Dolphins were soft and went for 2 when down 8 as an intimidation tactic. The Titans converted, the Dolphins looked sad and defeated, and the Titans went on to win the game.

It’s these nonprobabilistic elements that make football so fun. Strategies matter. Players who become superhuman are awe-inspiring. Football is not a controlled physics experiment. It’s not even poker. No one would watch if it was.