Modeling Dystopia
How do you deal with the paradox of choice in optimization modeling?
This is the live blog of Lecture 7 of my graduate class “Convex Optimization.” A Table of Contents is here.
Let me start off today with some of that dreaded linear algebra. The most important matrices in numerical computation are the positive semidefinite matrices. A square, symmetric matrix is positive semidefinite if all of its eigenvalues are greater than or equal to zero. In today’s class, I’m going to describe how almost all of the problems in Boyd and Vandenberghe can be posed as
Here Ai are all n x n matrices. n is whatever integer you want, but you should try to keep it as small as possible in your modeling. This problem is called a semidefinite program (SDP).1
Semidefinite programming generalizes linear programming to the positive semidefinite cone. In linear programming, the constraint “Ax≥b” is the same as writing
In SDP, we’re just swapping nonnegative vectors of LP for positive semidefinite matrices.
The range of problems you can write as SDPs is amazing. Any linear program or convex quadratic program falls under the hood. Minimizing a univariate polynomial on the unit interval can be posed as an SDP. You can even pose ordinary least-squares as an SDP. Instead of solving
you can solve
You shouldn’t solve it this way.
Let me be very clear here: I think it’s important to learn about SDPs and their generality and their relationship to convex programming more broadly. But my general advice is to avoid SDPs at all costs. At the end of the class, I’ll describe general algorithms for solving SDPs. They technically run in polynomial time, but it’s a pretty big polynomial (O(m^6), maybe? It’s so large I’ve blocked it from my memory). If you tried to solve all of your problems with SDP solvers, you’d be waiting a very long time.
One of the utopian ideas of optimization research is that we can develop modeling languages that can parse the high-level models posed by practitioners into code efficiently executable by optimization solvers. Since the 1970s, people have proposed different algebraic modeling systems for this task. This ideal was a substantial motivation behind Boyd and Vandenberghe’s text. The ambitious agenda was that disciplined convex optimization could solve the solver interface problem for a huge set of relevant models.
Despite the captivating vision, no universal modeling language ever really panned out. Someone should write a longer article examining the history of these languages and why they failed to capture broad adoption. There’s an important lesson for the optimization community in understanding why PyTorch became super popular, but GAMS remained niche for 50 years.
I have some guesses, but I need to think more about how to tell a coherent story. I’ll give a few scattered initial thoughts. First, I think targeting multiple solvers is problematic. Optimization often feels like a zoo of methods. Solvers force your hand in formulating problems in very particular ways. If you want to use gradient descent, you have to model everything as a giant objective function, eliminating the constraints. You might then try to use projected gradient descent, but this requires knowing how to project onto sets. Hence, you’d be limited to modeling your problem as an objective function subject to a single constraint that you choose from a limited menu. If you have a linear programming solver, you work to formulate your problem as a linear program. If you want to minimize a quadratic cost with your linear constraints, now you need to go and find a quadratic programming solver. And so on and so on.
There are too many equivalent ways to pose optimization problems, and we have no way of knowing in advance which formulation will be solved most efficiently and accurately by the solvers we installed on our workstation. This is even true if all we have is linear programming solvers. Software will solve two equivalent linear programs in vastly different times. Removing the practitioner from the solver interface forces them to invent weird tricks in the modeling language to get better performance. This leads to writing obfuscated models, betraying the ideal of letting modelers model in their natural language.
Matching numerical solvers to problem instances is even a problem in equation solving. Suppose we just want to solve for x in the equation Ax=b. There is a zoo of different possibilities for this too. How many different routines are there in LAPACK? More perniciously, there is the problem of conditioning. Suppose A is a positive semidefinite matrix. Then solver performance will vary depending on the eigenvalues of A. If the largest eigenvalue is much larger than the smallest, solvers will get bogged down in convergence and numerical errors. These problems are called ill conditioned. Even in linear systems, you need to figure out how to pose the problems so the solvers won’t run into problems of conditioning.
I’ll come back to this question about why the modeling language utopia never panned out in future posts, but let me close with something more constructive. Steve Wright thinks that optimization is best approached like an old tool chest in the garage. You’re going to have a wide assortment of formulations and methods. Keep that assortment well organized in your head. Learn about what all of the tools are, how to use them, and when they are best applied. Not every home improvement project needs a 6-axis CNC mill. Sometimes you just need a screwdriver. If you get a good feel for all of the tools in your chest, you never need to call a contractor.
I can hear Jeff Linderoth groaning already.


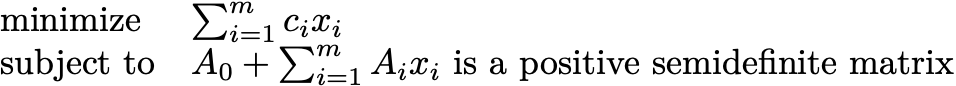
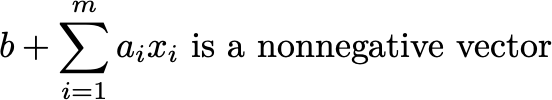
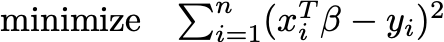

old tool chest in the garage is so based. Truly, this is the way
> There’s an important lesson for the optimization community in understanding why PyTorch became super popular, but GAMS remained niche for 50 years.
I would say there's a lot of software-specific and community-specific factors behind the divergent outcomes, to me it's not just a lack of a "silver bullet" modelling format in optimization. As you noted a while ago in the "Github descent" posts, one salient factor behind the rise of modern ML and DL methods is widespread code sharing, reuse, and comparison on different benchmarks. You can pip install pytorch and get ready to learn deeply in a matter of seconds, whereas if you run GAMS or AMPL you have to start by checking whether you qualify for some free license or another or have your employer procure it. Nowadays the open-source optimization stack has improved a lot, but there are still limitations. Let's say you work in Python: *
- You can use Pyomo, which covers a lot of what you want in a mathematical programming language, but whose performance is (or was) still a bit constrained by the interpretation overhead and the reliance on the AMPL NL library. For nonlinear stuff, if you use anything beyond the standard mathematical operations set you needed to manually build e.g. interpolants.
- You can use CasADi, which is great at what it does, but that does not cover any mixed-integer stuff.
- You can use something like Python-MIP which has a simpler syntax than Pyomo but, again, you can't go nonlinear.
- You can use Cvxpy, which implements Boyd's DCP approach, but then nonconvex operations or domains are out of the scope.
- You can use the GAMS bindings, but that's again commercial.
There is a project that is kind of covering all this space in a single modelling language: JuMP, which allows you to model all the problem classes I mention and even use external functions through the registering mechanism. The downside? You have to opt-in to Julia, which is nice but still niche. While it does not have all the bells and whistles of commercial systems (e.g. as I understand GAMS can do things like automatic exact linearization of binary products so that you don't have to manually reformulate), it does deliver a fully-featured open-source optimization modelling language. So I'm a bit more optimistic on the "MP language dream", even though I fully agree with the tool chest comment when applied to solvers (where the commercial / open-source divide is more striking than in the mathematical modelling libraries). The only caveat here is that, in many instances, you'd rather use a different interface for an optimization component that does not go through any modelling layer, but feeds itself the functions and derivatives to a lighter solver interface.
Now, if you use PyTorch, you don't just have a passable open-source solution: you have an industry-standard tool along with an ecosystem of open-source implementations for basically any DNN architecture ever published.
Another factor, I'd say, is the scope of the "optimization problem": things like "image classification" problems are all alike, but every optimization problem is a mathematical problem in its own way. This disparity makes it harder to achieve a critical sharing mass, especially when many of the most experienced researchers are working in competitive enterprise settings.
* Some of these impressions might be outdated, please correct me in that case.