Lakatosian Defense
Meehl's Philosophical Psychology, Lecture 5, Part 1.
This post digs into Lecture 5 of Paul Meehl’s course “Philosophical Psychology.” You can watch the video here. Here’s the full table of contents of my blogging through the class.
In Lecture 5, we get Meehl’s elaboration of “Lakatosian Defense.” This is the meat of the course and the core of what resonated with me. Meehl’s Lakatosian Defense is a tight metatheory that closely characterizes what I think most people mean by “the scientific method.” I plan to spend the rest of the week mulling over the many implications. I’ll discuss how Lakatosian Defense encapsulates everything weird we’ve seen so far in the course. I might even add some examples of my own. Unpacking the implications will require some careful meditation.
What are we actually testing when we test a theory? Let’s start with the naive caricature. We design experiments by creating a chain of deduction from the theory to a predicted experimental outcome. In the language of logic, we have a theory, T, and deduce an experimental outcome, O.
If the prediction pans out, we say the theory is corroborated. But if it doesn’t pan out, the theory is falsified. However, as we’ve been describing, this is far too simple a view to accord with the history of scientific practice. Meehl shows, however, that it’s not too far off. We just have to adjoin a bit of complexity to fully flesh out the scientific method.
First, Meehl presents a slight elaboration of what counts as a prediction. An experimental outcome is a material conditional “If I see O1, then I will see O2.” He writes this using the logical notation as “O1⊃O2.” This seems like a fairly reasonable starting point.
Let’s now turn to the theory “T.” An actual deduction chain from theory to this experimental prediction is a complicated complex of statements that Meehl breaks into five subsets:
TC - The theory to be tested. I’ve added an extra subscript C here that Meehl doesn’t use to denote “core.”
AT - Auxiliary theories involved in the derivation chain. These are all of the sorts of statements you use on top of your core theory. Anything you use to map the constructs of the core theory to the observables would count as an auxiliary theory. In particular, this includes the idealizations you know are wrong, whether idealizations of first principles or boundary conditions.
AI - Auxiliary theories about the instruments used in the experiments. Meehl separates these out declaring AI to be any auxiliary that’s not directly in the scientific field. If you’re running a mouse experiment, the mechanics of the lever the mouse uses to get food is an instrumental auxiliary. In medicine, you’d probably say that imaging devices or lab tests are instrumental auxiliaries. An unavoidable auxiliary in every experimental setup is software, whether for data storage, cleaning, analysis, running experimental protocols, or really anything else. Woo boy, is software a problem. Flag that for later.
CT - The ceteris paribus clause. Ceteris paribus is just the “all else being equal” clause we apply logically to an experiment that allows some notion of transportability of the results. What exactly we’re holding equal is not always clear. This statement asserts experiments are sufficiently controlled so that no unspecified outside factors influence the experimental observations.
CN - The particulars about the experimental conditions. This is a bit trickier to pin down but contains all of the ways a particular lab runs an experiment that are not cleanly bucketed into auxiliary theories. For example, Meehl described how rat handling could influence the outcome of latent learning experiments. It’s these sorts of conditions that maybe aren’t as cleanly specified that get lumped into CN.
Putting everything together gives us this logical representation of a scientific derivation chain:
The conjunction of the core theory, the auxiliary theories, the instrumental auxiliaries, the ceteris paribus clause, and the experimental conditions logically imply “If O1, then O2.” This statement is a logical statement. A scientific prediction is a logical deduction from the set of theories on the left-hand side to the material implication on the right-hand side.
It might seem like we haven’t done much in this development, but we now can neatly explain why falsification is so tricky. When you see a lot of O1, but not much O2, the right-hand side is false. We can now apply modus tollens and declare the left-hand side false. But what did we falsify? We didn’t falsify our theory TC. We falsified a messy conjunction. The falsification of the conjunction just means that at least one of the five terms is false. We don’t know which one. This is the starting point for Lakatosian Defense. If we are really committed to our core theory, we attack the other logical complexes from right to left, hoping they are to blame.
We first go after experimental conditions. This is where we demand replication. What if my rival scientist did something screwy in the lab? If the result replicates, perhaps we can attack ceteris paribus, finding some other unspecified cause that explains the outcome. We could attack the instruments, claiming there was a bug in the software, the wrong application of statistics, or a heat artifact in the measurements. We could attack our idealizations, creating a longer derivation chain that explains away the potential falsifier. We could attack other auxiliary theories. There are so many things we can defend and rationalize before we ever decide our theory is wrong.
But if we can continually churn out experimental results, why would we abandon our theory? This is the one missing piece in the scientific method as presented thus far: It’s not enough to imply obvious experiments. We need our theory to generate novel and surprising facts. To account for this, Meehl adds one last piece to the implication: we must derive experimental outcomes such that, given our background information, the probability of O2 conditioned on O1 is small. That is, our theoretical derivations must result in Damned Strange Coincidences. In this case, when we observe O2 given O1, the theory is corroborated.
This completes the picture. Scientists derive clever experiments. They test their predictions. When the predictions pan out and are Damned Strange Coincidences, they give Ted talks. When they don’t pan out, they attack their rivals.
Lakatosian Defense gives us a rational justification of scientific irrationality. You can already see how scientists could continue an infinite regression (also known as a career) of theory-building and experimenting while never abandoning their core superstitions. There is no end to fighting about experimental conditions, looking for hidden causes, or creating monstrous theories with unbounded free parameters. But it’s “rationally justified” as long as it’s producing new facts. Science is a paperclip maximizer.


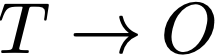
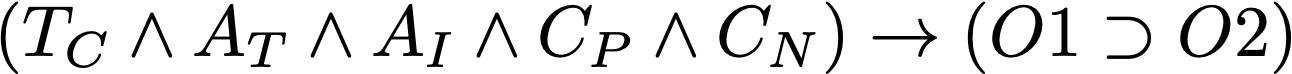
This is like a TV series in which every episode ends in a cliff-hanger!
That last paragraph is so spot on, loved it!
However, there is something I would love to understand and maybe I am lacking some basic thought here, but why does the appearance of O2 corroborate T? If O2 is very very rare, couldn't it also be a random occurence forcing us to second-guess all the other left-hand factors as well?
Furthermore, why, if T says O1 -> O2 is going to be very very rare mean that when we see O2, the theory is right? Shouldn't it be rather the other way round that when T says O1 -> O2 is extremely rare, we could assume that there is another T* or A or C which is responsible for generating O2 and such should maybe relegate all O2 to uncontrolled / parallel mechanisms?