In Defense of Defensive Forecasting

Is superforecasting just sneaky accounting?

I’m excited to share a new paper with Juanky Perdomo that surveys an underappreciated, powerful perspective on forecasting. Our opening paragraph sums it up.

“From sports to politics, from the stock market to prediction markets, from cancer detection to sequence completion, prediction is a big business. But how can someone get in on the action? A forecaster is only as good as their record, so they must demonstrate that their predictions are prescient. To make good predictions, it seems like you need some level of clairvoyance to see what the future holds. But what if forecasters can cleverly cook their books to make their predictions look good? What if they could make predictions that correct the errors you made in the past? In this case, they wouldn’t need to know anything about the future. They’d just need to know how to do proper accounting. In this survey, we describe a simple, general strategy for such strategic accounting, Defensive Forecasting.”

The term Defensive Forecasting was coined by Vladimir Vovk, Akimichi Takemura, and Glenn Shafer in a brilliant 2005 paper, crystallizing a general view of decision making that dates back to Abraham Wald. Wald envisions decision making as a game. The two players are the decision maker and Nature, who are in a heated duel. The decision maker wants to choose actions that yield good outcomes no matter what the adversarial Nature chooses to do. Forecasting is a simplified version of this game, where the decisions made have no particular impact and the goal is simply to guess which move Nature will play. Importantly, the forecaster’s goal is not to never be wrong, but instead to be less wrong than everyone else.¹

To be somewhat precise, in the forecasting game, the forecasters are tasked with predicting a sequence of events. For today, let’s say the questions have yes/no answers. Will it rain in Peoria tomorrow? Will Dorcey Applyrs win the mayoral race in Albany? Will the Dayforce stock price drop below 50 in June? Will Scott Alexander get his bloodwork done this year?

For each of these predictions, rather than giving a yes or no, we’ll let people answer with a real number, p. We’ll score these numbers based on a rule that everyone knows in advance. A popular rule is the Brier Score where, for each predicted event, the forecaster gets (1-p)² points if the event happens and p² points if the event doesn’t happen. Other people like other scores. The point is that the scoring rule is known in advance to everyone who wants to play the forecast game.

Once we settle on the moves and scoring system, the game plays out in rounds. In each round, Nature reveals some facts about the world to the forecaster. The forecaster makes some predictions about the outcome of a set of events. Nature then chooses the outcomes of the events, and these are revealed to the players. We tabulate the scores and move on to the next round.

How could you win this game? You don’t need to be Nostradamus, but rather just better than everyone else given the information that’s out there. This is a different goal! Maybe you can just be a sneaky accountant who is looking at other people’s answers and hedging your bets.

Juanky and I describe how, in most setups people use, this is indeed the case. You can make predictions by correcting past errors. Figuring out which prediction to make can be reduced to a simple binary search problem. And these simple searches that correct past errors achieve theoretically optimal bounds based on the information gathered during play. If you know how you will be scored and what your competitors will be using to make predictions, you don’t have to “know what nature is going to do” to be a superforecaster. You can get good prediction scores just by correcting your past errors.

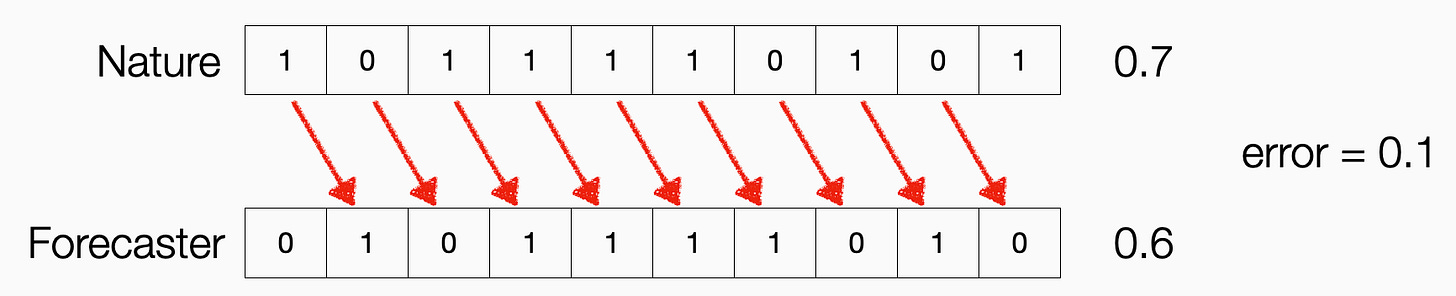
Let me make this very concrete with a simple example that Juanky and I work out in painful detail in Section 2. Suppose we’re just trying to predict the free-throw percentage of a basketball player. We’re scored by how accurately we guess their rate of success. Then the optimal prediction for the next free throw attempt is whatever happened on the last attempt. If they hit the shot, predict they’ll hit the next shot. If they miss, predict they’ll whiff. This strategy is correcting past errors: you are simply cancelling the cross terms in Nature’s average, as I show in this picture:

Here, the top row lists the actual outcome of the event. The bottom row lists the predictions. Each prediction in the bottom row is made to cancel out the previous outcome in the final average. Hence, when you take the difference between what happened and what you predicted on average, you only pay a cost for the first and last event in the sequence. The more predictions you make, the better your score looks.

This ability to error correct seems like it might be a pathology of this particular simple forecasting setup. We show this is very much not the case. Generalizations of this example give simple and powerful algorithms for a variety of interesting problems, including online learning, debiasing, calibration, prediction with expert advice, and conformal prediction.

Now, when you think about it, all predictions are functions of the past, not the future. If you are predicting someone’s likelihood of making a free throw based on their past attempts, you are always using the past to predict the future. However, Defensive Forecasting tells you how to make those predictions once you know how you’ll be scored and what types of data summarization tools will be available to you. The winning strategy is to use your prediction not to guess what Nature is going to do, but to make your past predictions appear more accurate. The key is to do this accounting in such a way that, no matter what Nature does, you come out ahead of everyone else in the end.

Over the next week or so, I want to dig into more about why I care about forecasting and how it’s solvable by bookkeeping. This connects back to one of the most important lessons I took away from my evaluation class with Deb Raji: our evaluations determine our algorithms. Defensive Forecasting is a prototypical illustration of this metrical determinism. Laying out the rules of the game dictates which algorithms you should use.

But these strategies also call into question what forecasts are doing in the first place. Why do we care so much about being superforecasters? Which questions are we asking? Why are we asking them? And why should we trust superforecasters if their predictions can be automated by Excel macros? The forecasting gurus want to impress you with their card tricks to fool you into trusting their authority. Don’t.

1. Yes, I see what I did there.