Heaven or Las Vegas?

All roads in the probabilistic universe lead to betting.

Yesterday, I mused that while it is impressive that Kolmogov’s axioms describe dozens of different conceptual notions of probability, many mathematical abstractions also describe myriad real-world phenomena. But I wondered if there was any truly unifying concept where the many notions of probability ended up being the same. I think the answer is both sad and obvious: they all agree on fair betting odds.

When mathematicians see a probability, they assume they can generate random samples. This is what connects the abstract axioms to the real world. Take, for example, von Neumann’s game theory. The key mathematical result in von Neumann’s paper is the minimax theorem. And the key conceptual jump needed to prove the minimax theorem was the mathematical abstraction of a mixed strategy. 

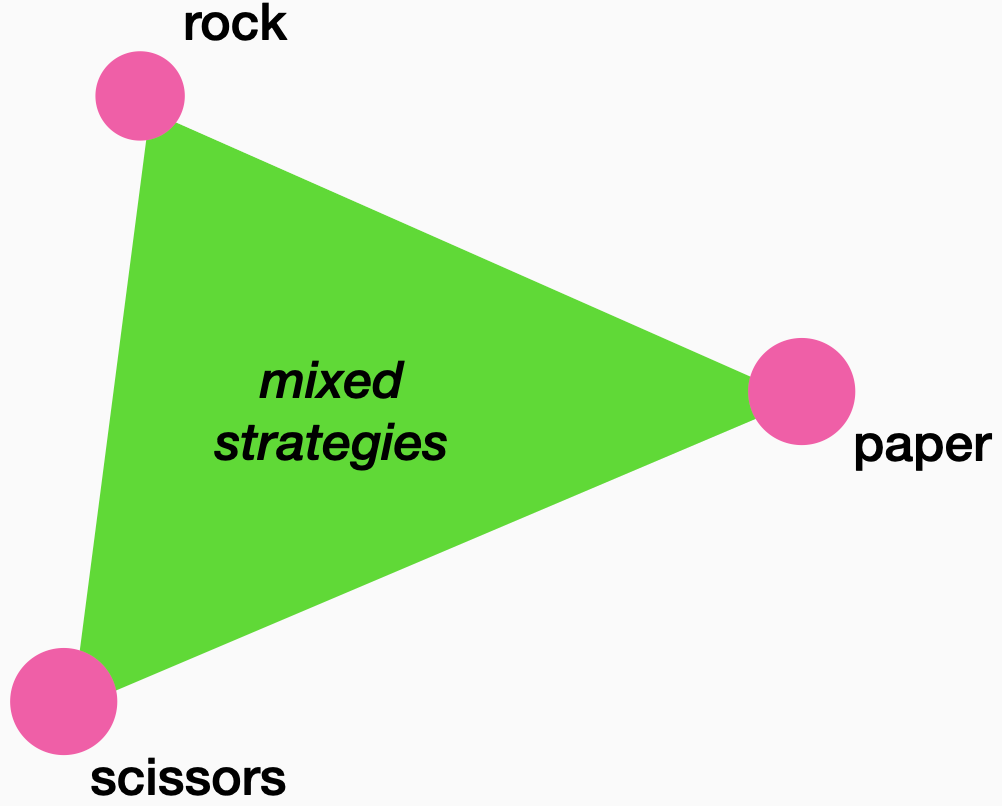
Abstractly, we can represent each pure strategy in rock-paper-scissors as the corner of a triangle. We can then declare that all of the points inside the triangle are strategies too. Mathematicians are free to assert what they want as long as the proofs follow deductively from their assertions. When we are allowed to use such mathematical objects, there are points inside the triangle where both players are equally likely to win.

Now, how do we turn one of these abstract interior points into an actionable strategy? We can express every point inside the triangle as a convex combination of the corners. That is, we can find weightings of each corner that give us the point inside, and the weights are nonnegative and sum to one. But if the weights are nonnegative and sum to one, we can declare them to be functional probabilities and sample the corners by these weights. When we do, this means that the average point we get after repeatedly playing the game is our desired interior point. An abstract convenience, a point inside the triangle, becomes an actionable option through sampling.

If I have a probability space, I can imagine sampling from it. Kolmogov’s axioms allow for a mental transmutation through sampling. If you have a probability distribution, this implies a generative process. And if I know how that generative process creates random samples, I can bet on the outcomes. If I know that events have certain odds, I know how to maximize my expected winnings. 

Anyone who’s ever played with Monte Carlo samplers knows that just because you can imagine random samples does not mean you can generate them. Probability requires computing a lot of integrals, and we all know from calc 2 that integration is hard. But theoretical computer scientists have shown that integration is really hard, often landing us in weird complexity classes like #P that only a rarified crew understands. I don’t really understand this 150-page paper, but it argues that if you can sample from the associated distribution, the “polynomial hierarchy collapses.” How much would you bet that the polynomial hierarchy collapses?

Regardless of these computational concerns, the point is that probability lets us imagine sampling, and if we can imagine sampling, we can imagine betting. And we can think about betting on all of the examples I listed yesterday:

1. Any finite list of numbers that is nonnegative and sums to one

2. Any infinite list of numbers that is nonnegative and whose infinite sum converges to one

3. Any nonnegative function on the unit interval whose integral is equal to one

4. The certainty of logical propositions being true 

5. The doubt that something in the past happened

6. The likelihood that future events will occur

7. A person’s internal beliefs about the world 

8. The relative frequencies of occurrences that currently exist in the world

9. The relative frequencies of hypothetical infinite populations

10. The preponderance of evidence in a civil case

Examples 1-3 are mathematical probabilities that we can sample from. Examples 4, 5, 6, and 10 are metalinguistic beliefs that someone could run a prediction market on. Example 7 has the whole Dutch Book argument associated with it, for better or worse. Examples 8 and 9 are our standard frequentist ideas that we use to calculate the odds of actual casino games. 

I’m not arguing here that the Bayesians are right. No one is right about the unknowable! I’m not saying that these ten ideas are all equivalent to betting. I’m just saying that the concepts all line up when we open up the DraftKings app. Betting is what ties the languages of chance together. It lets us tie together the threads of the series: any convex combination is a probability (von Neumann), we can sample from arbitrary distributions (Pearson), but in reality, anything is a sample (Fisher), hence I can tie my beliefs about outcomes to real events (Ramsey), but that means I can compute the expected cost of any outcome. I am Jack’s Complete Lack of Surprise. I am now an Effective Altruist.

I’m not even joking about this last part. In the probabilistic view of reality, every action is a gamble. Any colloquial statement about probability, chance, likelihood, or certainty means that there are real numbers out there associated with the assertion. It’s not too much more of a logical leap to associate a cost with each potential outcome. Weight the costs by their probabilities. Sum them up. Get expected values. It’s inevitable that particular choices will lead to more utils. It’s now clear that p(doom) is 10%. Or whatever. 

You can see how a person who spent too much time in online poker rooms or fantasy baseball thinks they can put odds on the outcomes of elections and other one-off events on their wildly popular blog. For the probability-pilled mind, the universe is a casino. May the odds be ever in your favor.