Growing Evidence

Meehl's Philosophical Psychology, Lecture 8, part 4.

This post digs into Lecture 8 of Paul Meehl’s course “Philosophical Psychology.” You can watch the video here. Here’s the full table of contents of my blogging through the class.

The second theme of Lecture 8 is moving beyond significance testing altogether. Hear hear. I worry that science reformers spend too much time asking for rigid, robotic “repeatability” of the same experiment rather than creatively thinking through the different potential predictions and consequences of the same theory. Repeatability spends too much time trying to nail down the experimental conditions clause in the derivation chain. We need ways of probing higher up the chain, among the auxiliaries and theoretical constructs. This can only happen by generating and testing diverse, risky predictions.

Indeed, Meehl thinks we are overly optimistic about what we prove when we do a significance test. As we’ve discussed, significance tests only evaluate whether a treatment is more correlated with the outcome than pure randomness. If I tell you “under the assumption that the treatment was a completely random assignment and didn’t do anything, the probability of seeing your result or greater is 5%,” what do you conclude exactly? What did you corroborate?

The most common reply I get when I rant about the bizarre primacy of Fisher’s exact test is “People have to do something, no? You are arguing for doing nothing.” This is a strawman neither Meehl nor I subscribe to. There are so many possible ways to reach a Damned Strange Coincidence, but having to stick a p-value on them squeezes our brain into thinking about the most primitive sorts of tests, ones that don’t tell us much of anything. Of course there are other things you can do! Meehl puts it this way:

“We are overly optimistic about what you prove when you do a significance test, but when pressed to do something more than that, psychologists and the soft areas at least tend to be pessimists about whether you could do any better than that.”

Meehl’s ideal case, which perhaps might be asking for more than we can get, is the sort of point predictions you might get from a physical theory. A theory that can predict diverse outcomes to high precision. 

While they are important and worth learning, the physics examples are wanting. First, getting the same precision as classical mechanics is likely out of the question in social science. To his credit, Meehl had put forward various suggestions of imprecise predictions that would be informative. For example, in the abstract of his famous “Theoretical Risks and Tabular Asterisks” paper, he writes

“Multiple paths to estimating numerical point values (“consistency tests”) are better [than significance tests], even if approximate with rough tolerances; and lacking this, ranges, orderings, second-order differences, curve peaks and valleys, and function forms should be used.”

Second, while fundamental physics had an unprecedented run of success from 1800 to 1970, it has been in a rut since 1970.¹ We should find inspiration from other fields to provide useful suggestions for human-facing sciences. Let me now give one of my favorite examples from the human-facing sciences.

In 1906, biochemist F. Gowland Hopkins was investigating the essential chemical composition of sustainable diets. As was the style at the time, he ran controlled rat studies comparing the value of different diets. In one such study, Hopkins fed a control group only bread and the treatment group bread and a tiny amount of milk. He charted their weight for 18 days and then swapped their diets. The following plot won him a Nobel Prize.

In this plot, each dot is the average weight of a rat on a particular day (the x-axis is days, the y-axis is grams). The white dots mark the bread-only group, the black dots the bread and milk group. It’s beyond evident there is some component of the milk needed for growth. The fact that when you switch the groups’ diets, you see a trend reversal is particularly compelling. The group withheld milk always fails to thrive. There is something necessary for growth in the milk. Today, we know it as Vitamin A.

I guess we’d call Hopkins’ experiment a “crossover design.” But how would you compute a p-value? What’s the right way to test whether two growth curves are “statistically significantly different?” I don’t think statisticians have a good answer for us! There have been plenty of proposals but no consensus answer. And why would you compute a p-value? It’s so clear that something is happening in this experiment. I suppose we could just compare the percentage growth between the treatment and control groups. I did this. Even though there were only eight rats in each group, the p-value of the t-test was 0. 

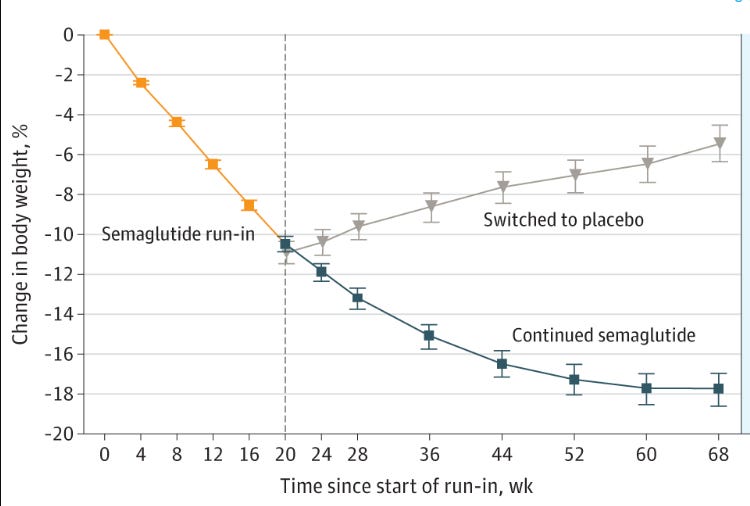
You might now say, “Well, we never find interventions with p=0 in our modern complex world.” But this couldn’t be further from the truth. Here’s a plot of growth curves I found in the New England Journal of Medicine in 2021.

This plot, of course, is from the clinical trial report on semaglutide. This curve tracks the average growth! It’s identical to Hopkins’ error-bar-free visualization. I love it.  Since this study had to conform to the rigid standards of the FDA and the NEJM, the paper reports discrete primary outcomes. They looked at the percentage change in body weight and whether weight loss was greater than 5%. And what’s the p-value for these outcomes? It’s “less than 0.001.” How much less? You can compute the z-scores of the endpoints by inverting the confidence interval. z equals 26 for the percentage change and 25 for the at least 5% weight loss. Anything over 7 means p=0. z=25 means p is very, very zero.

What do you think would have happened had they run a cross-over design like Hopkins? We know the answer as another 2021 trial reported in JAMA showed that switching from semaglutide to placebo resulted in weight gain. 

Though these are different studies, I think we can stitch the Damned Strange Coincidence together with our feeble inferential capacities.

Obviously, interventions like GLP-1 agonists come along rarely. But they do come along! And what’s weird about cases like this is that it makes you ask for examples of pivotal studies where p was 0.04. What about a rally pivotal study with p=0.01? If you have a favorite example, put it in the comments. And while we’re at it, what are examples in economics where z is more than 10? 

We should think about how we find and learn from controlled experiments with p=0. What can we learn from these discoveries? What are the different methodologies we’ve used to demonstrate such stark intervention effects (Damned Strange Coincidences)? What characterizes results where the statistics play no role in the corroboration? Just like historians of science think there are lessons to learn from the Newtons and the Einsteins, we have lessons to learn from the discovery of Vitamin A and semaglutide.

1. It’s a bit of a subcurrent in this blog series, but one of the ideas I’m most obsessed with is understanding a metatheory of science grounded in the successes since 1970. It’s quite possible we need something wholly new for the information age.