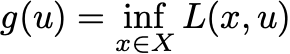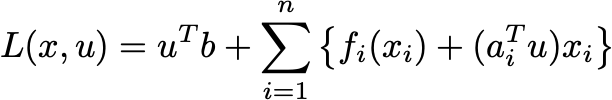Dual Decomposition

The tricks of the trade for running gradient descent on dual problems

This is the live blog of Lecture 21 of my graduate class “Convex Optimization.” A Table of Contents is here.

I’m taking a slight deviation from the book for the last lecture on algorithms this semester to introduce an algorithmic idea deeply rooted in the theory we’ve covered: dual ascent algorithms. These methods use convex duality to split optimization problems into bite-sized chunks that are easy to solve because they either have closed-form solutions or a very small number of variables. They also give simple paths to distributed algorithms and look like the schemes people use to train neural nets in parallel.

In a sentence, dual ascent is the gradient method applied to the dual function. In order to implement this, we need to figure out how to differentiate the dual. The answer is remarkably simple. Consider the primal optimization problem

Here, X is a convex set. Just as we have done in the past, we can introduce a Lagrangian for this problem

where u is the Lagrange multiplier for the equality constraints. The dual function is then

This is a bit different than the dual problems we studied earlier in the class as we optimize x over a set X, not all possible vectors. However, all of the earlier analysis applies here. Maximizing g(u) provides a lower bound on the primal optimal value. And under a Slater condition, there is no duality gap.

Suppose we want to optimize the dual function directly by local search. What’s a good search direction? Let z(u) be any point that minimizes the Lagrangian when u is fixed. Since the Lagrangian does not constrain z(u) to satisfy the equality constraints, Az(u)-b is nonzero. It turns out that this residual of infeasibility

is effectively a gradient of the dual problem. You can check that it provides a good linear approximation:

That is, v satisfies the same condition as the gradient does in the first-order convexity condition we derived early in the semester. With a bit of work, you can make this precise. Danskin’s Theorem states that if the infimum is attained at a unique point z, then g is differentiable at u, and v is its gradient.¹

This suggests a path to implementing gradient ascent on the dual problem:

Start at u[0] = 0. 
for k in range(T):
  Minimize L(x,u[k]) to yield x[k]
  Set u[k] = u[k] + t (Ax[k]-b)

When should you use dual ascent? In many cases, minimizing the Lagrangian is much simpler than solving the primal problem. A canonical example is when this algorithm decomposes the primal problem into simple-to-solve chunks, and the dual step stitches the chunks back together. Suppose we want to minimize a fun of scalar functions where the variables are constrained by equalities

Each function here is of a single real variable. Let a_i denote the ith row of A. Then Lagrangian can be rewritten as

You can minimize each term in the sum independently from each other. This means it runs in time linear in the number of components. Moreover, you can do these univariate minimizations in any order. You could run them on different cores and aggregate their answers to compute a new value for the dual variable. This method thus not only points to algorithms with fast iterates but ones that admit pleasantly parallel implementations. 

This algorithm is called the dual decomposition method. Economists love this algorithm as it helps them think about markets: you could imagine that each summand was the utility of an agent, and the constraints represented resource constraints. In this case, we could think of the Lagrange multipliers as prices (coughs in econ shadow prices) that enable the agents to optimize without coordination. Networking folks have used similar ideas to think about queue management protocols.

There are other applications of dual algorithms where we introduce redundant equality constraints to provide simple iterative algorithms. The problem

is the same as

but the redundant equality constraint in this reformulation buys us some algorithmic flexibility. If it’s the case that minimizing f and g on their own is easier than minimizing them together, dual ascent methods provide easily implementable algorithms.

The bummer about these dual methods is that they are slow. The problem is that dual functions are almost never strongly convex. Hence, the best we can hope for is a slow rate of convergence. On strongly convex functions, the gradient method converges to an ϵ-accurate solution in log(1/ϵ) steps. Without the strong convexity assumption, we can’t guarantee much more than 1/ϵ steps. That’s a big difference! 

You can get slightly faster methods with a bit more sophistication. Minor tweaks to the dual decomposition method yield the Augmented Lagrangian Method and the Alternating Direction Method of Multipliers (ADMM). These tend to be faster because they smooth out the landscape of the dual problem. I’ll cover these in class today and perhaps blog about them in more detail tomorrow.

But sometimes this slow rate is ok. Dual methods provide a simple way to roll your own optimization algorithms that take advantage of a variety of model structures. If you don’t need 10 digits of precision or if your iterates are so fast that a hundred thousand steps is faster than a Newton step, you should try out these methods. Just as we often ditch Newton’s method for gradient descent because of constraints on our algorithm implementations, dual methods might be just fine for your application. They are an important drawer in your optimization toolbox.

1. When the infimum is attained at multiple points, v is a supergradient of g. You don’t need to know that to understand the algorithms in this post. I hope my optimizer friends will excuse my imprecision here. I’d need another week of lectures to properly introduce subgradients. But I think you can get the gist without them.