Digitally Twinning
Justifying generative modeling and the principle of maximum likelihood
This is a live blog of Lecture 21 of the 2025 edition of my graduate machine learning class “Patterns, Predictions, and Actions.” A Table of Contents is here.
The last few lectures of the class cover reinforcement learning in generative models. Rants incoming after Thanksgiving. But before I get to griping about reinforcement learning, I have to at least address the object of the preposition in that last sentence: generative models.
Generative models are probabilistic simulators of data. These simulators often need to be probabilistic because of the nonuniqueness of acceptable outputs. This is true whether you are simulating thermodynamic processes or the textual responses of people to questions in natural language. If randomness makes your simulations more compelling, you should use it.
So how do you build a generative model from data alone? Let’s imagine we have gathered a dataset and want to construct a probabilistic model that mimics the behaviors observed in it. Then, among your design desiderata, we obviously want the probability of the collected data to be large in the model.
What if “high probability of the data” is our only objective? Our simulation will be a manipulation of a stream of random bits, written out in code. A generative model is just a piece of software that takes random bits and returns samples. We want to find the computer code that makes the probability of sampling the collected data as large as possible.
We can explicitly write all of our assumptions about the dataset in our code. These assumptions can be of convenience, co-designing the form of the model to yield simple optimization problems. For example, suppose the data can be broken down into a set of N items, x1, …, xN. Then, by the definition of conditional probability, we can break the probability into a product
The optimization problem that aims to find weights that maximize this probability is equivalent to the one that maximizes the logarithm of the probability. So we have an optimization problem
The reason I broke out the logarithm is because it neatly turns products into sums. In optimization land, sums are just much nicer to deal with. Since the logarithm is an increasing function, it does not change the value of the optimal code.
We can make this optimization more tractable by imposing reasonable structures on the conditional probabilities. Such structural imposition is yet another modeling decision. Since our goal is not to find a “true” model that generates data, but simply a simulator that appears to simulate data, we have a lot of flexibility in our modeling. For example, we might assume the x’s are independent, in which case, we have a simple sum of repeated terms.
We might assume that xi+1 only depends on xi, in which case I’d rewrite the conditional probability from N down to 1 and solve the problem
This would be fitting a Markov chain to the data. We might model xi as only depending on the last m xj. That is, xi only depends on xj if 0>i-j>m. We can declare some subsequences in the data to be independent of other subsequences. Or maybe you have some totally other dependency structure in mind that I can sketch out as a (coughs) graph on my whiteboard.1 We can optimize that too. The degrees of modeling freedom are innumerable.
This freedom is the fun part of generative modeling. I’m building the simulator here, and I can choose the structure of the conditional probabilities however I’d like. I just want the outputs to look good. I will write this structure into my code. I can even add a holdout set. I can maximize the probability of the training set over a variety of different modeling assumptions and select the model that maximizes the probability of the holdout set. I’ve now solidly put generative modeling to look exactly like what we do in prediction.
If maximizing the probability is your sole design objective, the resulting optimization problem is called maximum likelihood. You are finding the parameters so that your data will be representative when you sample from your model.
If you read Ronald Fisher’s paper on maximum likelihood, he did not imagine that you’d actually sample from estimated distributions. Fisher was looking for summaries, not simulations. He posited that out of all of the statistical model summaries out there, we might as well choose the one under which the data had highest probability. I mean, sure. Statisticians spent the next hundred years trying to come up with convincing justifications of Fisher’s idea. Doob showed that for descriptive modeling, you can think of maximum likelihood as empirical risk minimization where the loss function is the KL divergence between your generative model and the true data-generating distribution. From a different direction, Shannon motivated maximum likelihood with notions of entropy and compression. All of these are fine, but the reason scholars spilled so much ink justifying maximum likelihood is that engineers wanted to use models for some sort of analysis or inference about the world. But validating probabilistic models is a murky mess.
By sharp contrast, the generative model problem gives a pretty brain-dead motivation for maximum likelihood. You just want to mimic data convincingly.
Now, I have real beef with statistical models, especially as they are used in applied statistics, and I’m on here yelling about them all the time. Statistical models as summaries without convincing simulations—what Fisher first envisioned in his maximum likelihood paper— should be held in high suspicion. If you think linear logistic models are good summaries of human behavior, you are delusional.
However, if your goal is to actually simulate, probabilistic models have many uses. Probabilistic simulations that pass the interocular trauma test are way more useful than anyone could have imagined five years ago. Generative modeling gives the strongest argument for the principle of maximum likelihood. You have to hand it to machine learning.
IYKYK.


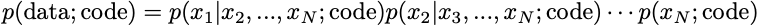
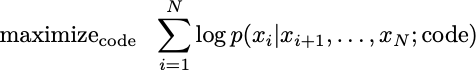
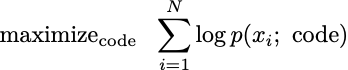
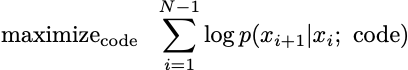
Agree with all of this (as usual). Yet it is a little unsatisfying as they are not the same level of abstractions. Perhaps statistical summaries solve an important inverse problem if the model is correct… but what problems do generative models reliably solve?
Hopefully it is a safe space to ask this away from the AGI pilled. I have some hot takes, but want to hear yours!
Sure, [strong] generative models are useful if you want to simulate data.
But I think "summaries without convincing simulations [...] should be held in high suspicion" is too strong. At the very least, expressive/strong generative models should be taken with just as much suspicion if literally treating them as "a model for how the real data was generated"!
The ultimate question, which is a hard one, is what do we want out of "a model". Obviously this is not an easy question to answer.
The way I see it (people might disagree) is that back when contemporary deep learning was reborn, after the initial excitement, many people started noticing the shortcomings (adversarial examples, brittleness, etc) and a rather common thought or excuse was: "sure, but this is only because we train discriminative models. We need to be training Generative models and _then_ you'll see that we will get _real_ human-like understanding, of latent variables and causal factors and all".
Over the past ~5 years a *lot* of effort (research, compute, funding) has been put to test this hypothesis. And I would say (again, people might disagree) that it has been largely proven wrong. Turn out that with enough data, you can _generate_ in completely convincing, non-trivial, domains (images, text, ...) **without any real understanding** (I'm not going to debate what "real understanding" is here, though). In fact I think this is, perhaps, one of the more significant scientific discoveries that came out of contemporary Deep Learning. This is even before current LLMs -- take Machine Translation for example. For ages, people argued very strongly (and with what sounded like very good arguments) that the only way to get a real, functional, automatic translation was for systems to have a real understanding of the text. Turns out that this is wrong. Same for image generation, and even video generation (despite the ridiculous attempts to call large video models "physics simulators").