Controlled Chaos

Perfect adaptation, overshoot, and stress response

I have been belaboring a bunch of linear systems theory in an attempt to get at something fundamental about homeostatic systems. Last time, I discussed how any system that regulates a signal to be constant contains an internal state that integrates the deviation from constancy. Today, I want to explore a consequence of these necessary internal integrators.

Let’s start again with a linear model of homeostasis. To review, I’ve been assuming we have a system that regulates some signal y[t] and is potentially perturbed by a disturbance signal d[t]. The internal variables are represented by a state vector x[t], and these vectors change in time according to the update rules

x[t+1] = A*x[t] + b*d[t]
y[t] = c*x[t]

where A is a constant matrix and b and c are constant vectors.

Let’s work out what these values of state and output are, starting with an internal state at time 0. We have

and so on. We can combine these formulas to find the value of the regulated signal at time t.

For the signal to converge to zero no matter the value of disturbance or initial state, we need two ingredients. First, repeatedly multiplying any vector by the matrix A must converge to the zero vector. Control theorists say that such systems are stable. If you’ve ever taken a control theory class, you’ll know you spend most of the semester finding conditions under which systems are stable. I don’t want to dwell too much on stability here today but foreshadow that even stable systems can have pretty peculiar “unstable” behavior when interacting with uncertain environments.

The more interesting condition is that this sum converges to zero:

This has a surprising consequence.¹ Suppose that instead of a constant disturbance, the disturbance is a shock. That is, think about the case when d[0]=R but d[t]=0 for all time after that. In this case, assuming x[0]=0, the regulated signal evolves according to the formula

This response to a shock has a particular shape. If the shock R is negative, then since the sum of the output must equal zero, the response must necessarily be positive before returning to steady state. That is, the regulated signal can’t simply decay back to the desired setting of zero. It must necessarily overshoot and become positive before returning to zero. There are many ways that this over-correction can happen. Here’s one possible shape for the signal

But the system could also potentially oscillate as it returns to steady state.

Are these behaviors biologically plausible? Not only are they plausible, but they are ubiquitous. It’s a bit weird to think that biological systems ring in response to shocks, but ample evidence exists showing oscillatory behavior from glycolosis in yeast to immune responses in mammals. A lot of the papers I’ve come across on biological oscillation attribute the cycles to “chaos,” but simple linear systems can also oscillate when acting as regulators.

The non-oscillatory overshoot mimics higher-level patterns in human physiology. Let me speculate on a connection here—one that I don’t think is entirely valid but also don’t think is entirely BS.

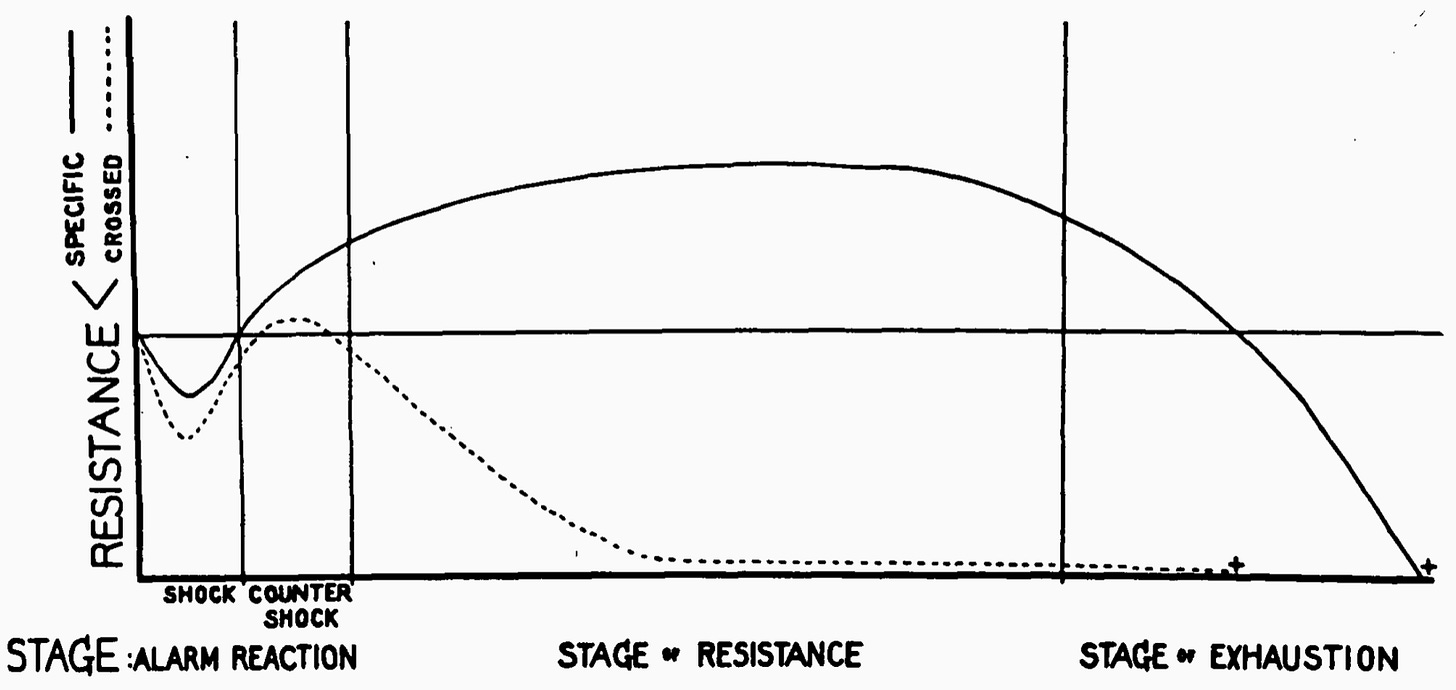
Overshoots in responses to shock have been noted in biology since at least the time of Cannon. In 1936, Physiologist Hans Selye proposed the concept of General Adaptation Syndrome, a qualitative temporal model for shock response. After an applied stressor, the body would initially be weakened, but it would mount a counteroffensive against the shock. This shock response, which Selye called stress, would eventually overcorrect and build a resistance to the threat. The resistance stage would last until a period of exhaustion, after which the body would perish.

Here’s a diagram from Selye’s paper that depicts his qualitative view of the stress responses he observed in the systems he studied.

Hmm. That certainly looks like the overcorrection we predicted using simple axioms for perfect adaptation.

Selye’s model of stress response had a profound impact on medicine. Notably, it was one of the first to characterize the physiological basis of stress, which we now take for granted.

Paradoxically, Selye’s characterization of stress also formalized a paradigm of treatment: introducing stressors to improve bodily function. If you stress a body and it overcorrects, then stressing the body again during the overcorrection can lead to further overcorrection. As long as the body never hits the “exhaustion” phase, it can improve in its response to stress. Repeatedly and appropriately stressing a patient can lead to their improvement. In physical therapy and strength training, this approach is called progressive overload. If you’ve ever spent time on fitness YouTube, you’ve heard this phrase bandied about. The necessity of overcorrection in homeostatic systems suggests such therapy can be widely applied. And here perhaps we find a path to connect science and bro science.

1. Again, my control theory friends, this is just saying that the system has a zero at z=1. In continuous time, the corresponding result would be a zero at s=0. The last couple of blogs have been a belabored way of emphasizing that a zero at s=0 is necessary and sufficient for rejecting step disturbances. This is a classic result, but it has important consequences for the possible impulse responses.