You're probably right
The value of randomized algorithms depends on verification.
This is a live blog of Lecture 15 of the 2025 edition of my graduate machine learning class “Patterns, Predictions, and Actions.” A Table of Contents is here.
This week transitions between the “predictions” and “actions” phases of the course. I want to talk about experiment design, bandits, and reinforcement learning. All of these require a bit more probability than normal machine learning. In particular, confidence intervals are unavoidable in RCTs and stochastic online learning. So I feel compelled to at least spend a lecture talking about them. And before confidence intervals, I need to bang the table about the value (or poverty) of ex ante guarantees in statistics.
So many results in machine learning theory and computer science more broadly are stated probabilistically.
“With probability at least 95%, this algorithm returns a decent answer.”
I’m going to fix the probability at 95% throughout to venerate the scourge of Ronald Fisher. The term “decent answer” here is always context-dependent, and some versions of decent are more useful than others.
Take, for example, the algorithm quicksort. Quicksort works by recursively dividing a list into subsets at random. Some random partitions are bad, and the sorting will take n2 operations for lists of length n in the worst case. But with probability at least 95%, this algorithm runs in time O(n log n).
Stochastic gradient descent is similar. For any ordering of the data, cycling over the data many times will find the optimal solution. There are worst-case orderings that can take an exceptionally long time. However, we can write theorems that assert random orderings of the data converge quickly with probability 95%. Like quicksort, this means that the chance you pick an ordering that is as slow as the worst ordering is low.
In both of these algorithms, you are explicitly generating random numbers, and the guarantee tells you that most generations fuel the algorithm to run quickly. If you generate bad randomness, that’s a pity. But such bad cases can be made arbitrarily rare.
Another class of randomized algorithms is comprised of promise algorithms. I guarantee you in advance that a decent solution exists and provide you with a means of checking it. Your job is to generate something that passes the check quickly. A classic example of an algorithm like this is Karger’s min-cut. Perhaps more relevant to machine learning and signal processing, randomized sketching algorithms have this flavor. For example, the Johnson-Lindenstrauss Lemma says that if given n input points in Euclidean space of arbitrary dimension, you can find n points in a low-dimensional space where the distances between all pairs are approximately the same as in your input. In practice, you generate this low-dimensional representation by sampling a random linear projection in the input space into the low-dimensional space. You can generate such a projection, and then check if all the distances are preserved. If they aren’t, you can generate a projection again. Here, if there’s a 5% chance of the algorithm returning something bad, you can rerun the construction multiple times and know the chance of a string of bad results is exponentially small.
PAC Learning is also like this if you can generate new data, with the twist that now the verification is probabilistic. In the PAC-Learning model, you sample n points iid from a distribution and run a machine learning algorithm on them. The guarantee is that your average loss on new data from the same distribution will be less than some number. You can probabilistically verify this guarantee as long as you have access to new data from the same distribution. This sort of logic was the basis of our statistical analysis of the hold-out method a couple of weeks ago. Of course, if you don’t generate the data iid or you don’t have access to new data, PAC bounds aren’t worth much.
Finally, sometimes we’re given the guarantee of decent solutions, but have no way to verify whether or not the solution is actually good. This seems pretty useless, if you ask me! And yet, far more people than you’d expect seem perfectly fine with such unverifiable algorithms. My favorite horror-show example of this class of randomized algorithms is the confidence interval.
A confidence interval is an algorithm that takes input data and outputs a set. The guarantee goes
“With 95% probability, the sampling distribution produces data such that the set output by the algorithm contains a parameter you care about.”
Here’s a canonical example. You flip a biased coin n times. You compute the empirical rate of heads, p. You then assert that with 95% probability, the true bias of the coin lies in the range
Now what do I do with that? I can’t check whether my sample was among the 95% of the good samples. I only know before I collect data that 95% of the samples are good. The guarantee on the confidence interval is ex ante. Ex post, there’s really nothing we can say about it. Do I know the true bias lies in that range? Absolutely not.
So I just call it a confidence interval and pat myself on the back. I’ve written before that guarantees like this have some practical purpose, but only in bureaucratic settings. We can agree in advance that you can get a paper published or drug approved or code pushed if the interval turns out to be narrow enough once we collect the data.
For the rest of us, if we can’t act again and we can’t verify, I’m not sure what exactly we should take away from probabilistic results like this. As we move forward in the course, I’ll try to focus on the many places where we don’t have to settle for trust, but can verify the outputs of randomized procedures.


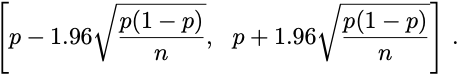
"venerate the scourge of Ronald Fisher" 🤣💀
This meager guarantee is also all you get from conformal prediction.