Your noise is my signal
Actuarial prediction from samples without features
This is a live blog of Lecture 3 of the 2025 edition of my graduate machine learning class “Patterns, Predictions, and Actions.” A Table of Contents is here.
Last time, I introduced two extreme cases in machine learning prediction problems. There was actuarial prediction where the same feature vector had many possible outcomes, but the features themselves had no particular relationship to each other. And there was interpolative prediction where each feature vector has only one outcome in a population, and we want to use similarity between these features to interpolate between the labels we’ve seen and the labels we’d like to predict.
I’ll come back to this distinction next week and have a lot more to say about interpolation. Today, let’s focus on the actuarial case and see why it’s actually not that different from interpolation. It turns out that for the metrics we tend to use, you only need a few examples to make good actuarial predictions.
My favorite example to motivate actuarial prediction is sports statistics. In particular, solo statistics like free-throw shooting. For a particular player, predicting the likelihood they’ll make a free throw can be well estimated from their history of free throws and not much else. Your confidence that a player will make a shot is based on how frequently they have made that shot before.
For folks who have taken classes on statistical modeling before, I want to emphasize that this prediction problem has no label noise. Every shot made by the player is labeled correctly. We have very good technology that detects whether a ball goes through the hoop. It does not make sense to talk about this problem as one of separating signal from noise in measurements. Instead, prediction deals with the fact that multiple scenarios that a statistician deems the same can have different outcomes. Our statistical lens clusters a bunch of different events together, and we’re forced to deal with the fact that our clustering has rendered these events indistinguishable.
Now, how do you numerify and evaluate your confidence in a free-throw shooter? The obvious answer to the first part of that question is to take the rate at which they hit their free throws and call this the probability they make their next free throw. Call this number p. But how do you evaluate this rate estimate?
You could first ask to evaluate the accuracy of your estimated free-throw rate. You could directly compare the mean rate over different time windows. That is, you could wait to see N free throws, and label a made free throw as y=1 and a miss as y=0. The difference between the rate you predict and the rate that occurs is called estimation error.
But you could also score your mean by computing its Brier Score.
The Brier Score is the mean-squared difference between the predicted rate and the actual events. This is called prediction error.
There’s a third way to evaluate that will be important later in the class. That is a sequential evaluation. In sequential prediction, you are allowed to make a different prediction for every free throw. You are evaluated based on your average success rate.
Your prediction pi can use all of the outcomes you’ve seen so far, from 1 up to i-1. This is online prediction where you are allowed to update your predictions as new information comes in. The earlier case we presented, where you can only use a single batch of data to make predictions about the future, is called batch prediction.
Interestingly enough, under most models we envision for how bits are generated, the score in both the batch and sequential settings is equal to the variance of y plus a term that goes to zero as the number of observations grows.
Here, the first term is the variance of y, and T is the number of observations. The variance term is unavoidable: even if you knew all of the outcomes in advance, the mean of those outcomes accrues a score equal to the variance of the sequence of the outcomes. It’s the irreducible error of the problem. All of the popular models of statistical prediction end up with an excess error because we estimate the frequency from a finite sample. The error miraculously always shrinks proportionally with the sample size.
Let me provide the simplest example, and you can check out the lecture notes for the other models. Imagine the outcomes are actually independent random flips of a biased coin. In this case, if you observe T flips and compute the frequency of heads, then the expected score is
Even with one observation, this score is within a factor of 2 of the best possible guess of the population frequency. With ten observations, the expected error is at worst 10% larger than the optimal error. Prediction is, in this regard, easier than estimation.
This same analysis holds if we collect a random sample from a population of outcomes, if the data generating process is exchangeable instead of iid, or even if we analyze sequential prediction where the outcomes are a completely arbitrary sequence. Actuarial prediction scores well with just a few observations. The process itself determines our Brier score: when the true rate is close to 1 or zero, we can get a low Brier score with very few examples. When the rate is close to 50%, we’re stuck with a poor score no matter what we do. The main difference between interpolation and actuarial prediction is this irreducible error due to statistical lensing. We’ll keep this in mind as we turn next to the more complicated question of interpolation.


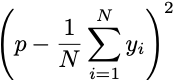
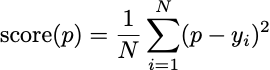
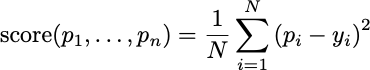
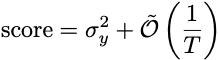
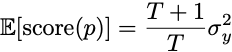
I took on the challenge of trying to find a more illuminating proof of your Lemma 3.2 about arbitrary bit sequences from the lecture notes
https://people.eecs.berkeley.edu/~brecht/cs281a/bit_prediction.pdf
With an assist from chatgpt, here's what I came up with
https://martingale.ai/bit_sequence_identity.html
Very interesting lecture! Looking forward to your next one on interpolation. I wonder if, intuitively speaking, if minimizing interpolation error should require us to find computable features that reduce variance in the outcome conditioned on the features, to connect with your derivation in this actuarial case.
You also mentioned that in real world we often have a prediction problem in the middle between the actuarial and interpolative extreme. Let’s assume, abstractly, our observations are casually generated by some latent variables of the system that the prediction would be considered actuarial conditioned on the latent variables, but interpolative conditioned on the observations. If we optimize our model by reducing prediction error using the observations, I wonder how likely is it we obtain features similar to the latent variables? In biology, the variance in your actuarial sense is the norm but I sometimes wonder if, with the overwhelming interest to train deep neural nets to interpolate data in our field nowadays, we are losing the grasp on mechanistically (whatever that means) understanding this inherent variability.