Three Causal Graphs

See how they run.

Last week, we discussed randomized experiments, a scheme for measuring the effect of actions by repeated intervention and measurement. But what if we can’t intervene? What if your advisor hands you some data and asks you to determine how certain variables impacted the others? What might you do? At this point, you enter into the nebulous and spooky world of observational causal inference.

The naive approach to estimating effects in a dataset would be to pretend an experiment had occurred. Suppose we wanted to understand whether drinking red wine reduced the incidence of heart disease, and we had millions of unstructured medical records for GPT7 to analyze. We could find all of the patients who said they drank around one glass of wine per day and count the number of heart attacks in their charts. We could find all of the patients who said they didn’t drink wine and make a similar count. And then we could compare the rates of incidence in the two groups. 

Why doesn’t this tell us if wine prevents heart disease? There are many gripes with this sort of study, but one is that there are a variety of factors that may cause heart disease and may be linked to the drinking of red wine. One possibility is that people of higher socioeconomic status tend to drink wine while people of lower socioeconomic status might not. We may also expect people of lower socioeconomic status to be more susceptible to heart disease for a variety of factors completely unrelated to wine consumption. But the naive correlation study wouldn’t be able to tell.

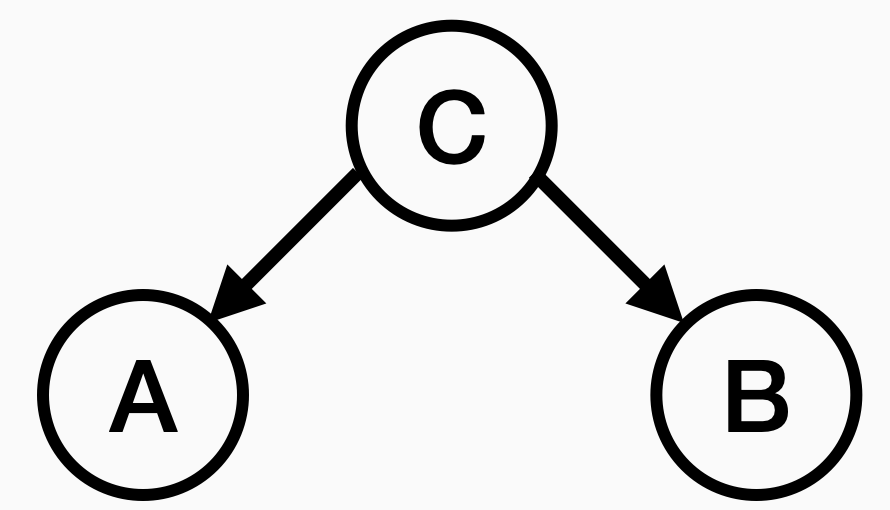
The above argues that socioeconomic status confounds the relationship between wine drinking and heart disease. We could summarize this dismantling of our nutritional study with a graph:

Node A could be the variable of consuming wine. Node B could be the variable of heart disease. Node C is the confounder, perhaps socioeconomic status. Here, the graph suggests that socioeconomic status, um, causes both heart disease and wine consumption. I am so hesitant to use the word cause here. Cause carries with it arrogance and conviction. I just mean that the graph demonstrates that the action we’re interested in (here, red wine) could have no relationship whatsoever with the outcome we’re interested in (here, heart disease), and yet the third variable associated with the action and the outcome will create an association when we compute statistical associations.

This graph we drew is called a “causal graphical model.” There is a bunch of fancy probabilistic machinery behind these graphs, but most of us can get by understanding the implication of the graph and never thinking about probabilistic graphical models. 

Two other graphs are critical to critiquing non-interventional studies. Here’s one:

This graph demonstrates a collider. In this case, the action (A) and the outcome (B) both influence a shared variable (S). If we choose a cohort to study the interaction of A and B by first selecting a bunch of records with the variable S, bizarre associations can arise. A and B can be completely independent random variables, but conditioned on S can become correlated. For example, think about hospitalized patients. Only the sickest patients go to a hospital. The fraction of people with severe cancer in the hospital is larger than the fraction of people with severe cancer in the general population. Because of this distortion of fractions, variables that are uncorrelated become correlated after restricting to people in a hospital.

This phenomenon, where fractions of extreme cases increase once samples are generated by selecting extreme cases, is called Berkson’s paradox or collider bias. Collider bias is confusing but ubiquitous! You’ll see collider bias everywhere once you drill yourself to look for it, and it explains so many spurious findings. For example, [studies during the pandemic determined that smoking prevented severe covid](https://www.nature.com/articles/s41467-020-19478-2). Oops. The result was spurious because it only looked at people in the hospital.

The final causal graph that’s important to recognize is the mediator:

Here, A only has an indirect effect on B through this middle node M. Mediators are mostly important because they are confused with confounders. If you use fancy techniques to remove the confounding effects of a variable (the term of art is “controlling for the confounder”), but the variable is actually a mediator, then you will diminish your estimate of the effect of A on B. Debate will then ensue about whether M is a confounder or mediator, spawning dozens of follow up papers.

There are many other causal graphs, but I don’t think we have to worry about them. The three covered today are the only ones you’ll need to demonstrate potential flaws in any observational data analysis. Certainly, people will add 200-page appendices to observational studies arguing that no colliding has occurred and all confounders have been accounted for. And then they’ll assert validity by using methods that identify causal effects when there are no hidden confounders. But there are always hidden confounders! If you didn’t do an experiment, some confounding had to arise in order for you to have this data frame open in your statistics software.

Oh boy, this week is opening a can of worms.

In the next lecture, we’ll discuss some of these methods for data-driven storytelling about cause and effect. Whereas randomized experiments are arguably the most important contribution of statistics, “observational causal inference through regression” may be the worst scientific methodology devised in the 20th century. It has convinced generations of researchers they could do science without experimentation. With the lone exception of debatably showing smoking causes cancer, it has done far more harm than good.

It’s mid-semester and I’m tired, so my vitriol level will be well below its usual eleven. I’m sympathetic to the idea that looking for clues in data can help inform decisions. Or at least it can help us pose better hypotheses to potentially investigate with more rigorous and controlled methods. But there are just too many degrees of freedom available to find anything sensible in an observational study. Not only can data be tortured until they say what the investigator wants, but the investigator can search for the dataset itself that proves their desired argument. Always remember, the hidden confounder in all of your observational designs is you.