The Soothing Warmth of Vacuum Tubes

Going back to the very beginning of feedback to understand its future.

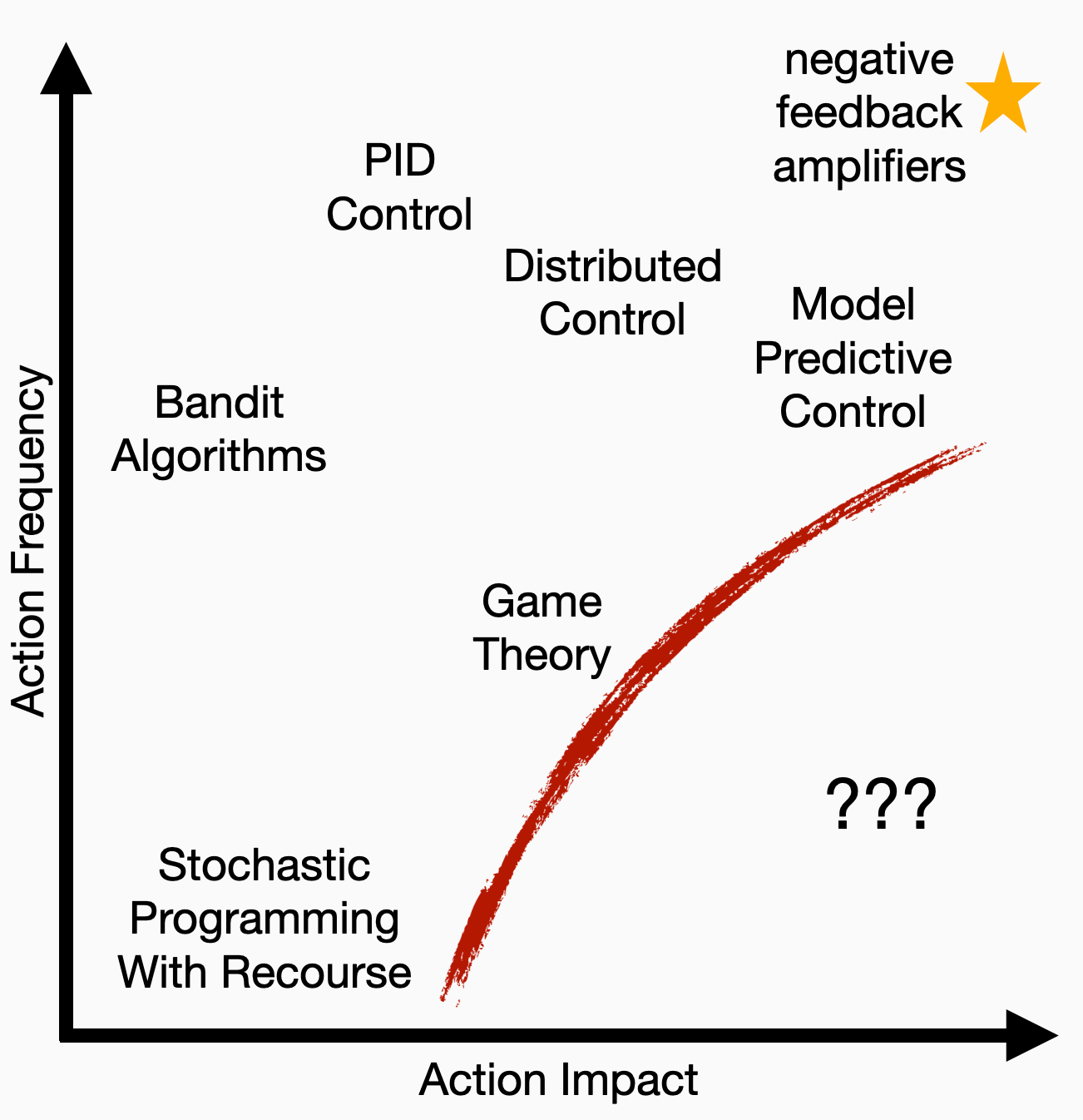
Coming back to this scatter plot of decision systems today, let’s jump all the way to the top-most corner:

What happens when you can act instantaneously with maximal impact? This is the realm of old school electrical engineering and the feedback amplifier. Though it’s a bit of a stretch to think of circuits like this as decision systems, they highlight some fundamental issues in a very elementary way. And the mathematics is just middle school algebra (I know this because I ran the post by my fifth grader, and he was into it.).

I have two circuits. The first circuit is a high-gain amplifier. This thing just takes inputs and makes them super loud. But I don’t know how loud the amplifier really is. On any given day, it might change its amplification level by a factor of two or more. And I’ve noticed that the amplifier is sometimes better at amplifying treble than bass, but sometimes it’s the opposite. The amp can make signals a thousand times louder, but it’s unreliable. Should I throw it out?

Maybe not. I have a second component, an attenuator, that takes signals and makes them slightly less loud. I can use the attenuator to make my unruly amplifier well-behaved by connecting the two parts in a feedback loop:

I can write what this circuit does as a few simple equations that link the inputs to the outputs. The amplifier is driven by the signal u. The voltage output of the amplifier is the amplifier gain times the input signal. This is the equation:

\(V_\mathrm{out} = A \cdot u\)

“A” is the amplifier gain I don’t know particularly well. The attenuator works by taking its input and reducing it by a factor of B. The corresponding equation of this effect is

\(z = B \cdot V_\mathrm{out}\)

Finally, the feedback interconnection rule subtracts z from the input Voltage to produce the input to the amplifier.

\(u = V_\mathrm{in} - z\)

We can combine these three equations into one, eliminating the variables u and z:

\(V_{\mathrm{out}} = A (V_{\mathrm{in}} - B \cdot V_{\mathrm{out}})\)

Now I can solve for Vout and get the final expression:

\(V_\mathrm{out} = \frac{A}{1+AB} \cdot V_{\mathrm{in}}\)

Let’s stare at this formula for a bit to see what it implies. First, as we make A larger, the gain from V_in to V_out approaches an asymptote. For super large values of A, the gain is basically just 1/B. But this feedback loop is very insensitive to the actual value of A. Suppose the attenuation factor B is ½. Then, when A is large enough, the gain should be around a factor of 2. We can plug in specific numbers and see a remarkable range of stable behavior.  If A = 10,000, the gain from V_in to V_out is 1.9996. If A = 20,000, the gain is 1.9998. If A = 5,000, the gain is 1.9992. Over a huge range of open loop gains, from 400 to infinity, the gain of this system is within less than 1% of the ideal gain. Despite vast differences in open loop behavior, the closed loop behavior is predictably the same for all of these different amplifiers.

It’s even better than this. I told you earlier that the amplifier was temperamental and might change its amplification on any given day or might amplify different signals to different levels. Suppose that the amplifier amplifies one signal by 10,000 and one by 20,000. Both signals will be amplified by 2 when put through the feedback circuit. We mitigate all sorts of uncertainty in one component with the simple negative feedback law.

So what’s the catch? Though we are insensitive to the amplifier, we’re very sensitive to the system we’re using to control the amplifier. The output gain is very sensitive to the attenuation factor B. If the attenuator changes by a factor of 2 from ½ to ¼, then the closed loop gain changes from 2 to 4. The attenuation circuit can be precision manufactured if a precise amplification is necessary. But variability is often desirable, as you might have a knob that changes the attenuation value. This would give you a volume knob. Turn it up to 11. 

There are less obvious, more dangerous issues. The feedback equations I wrote above assume the feedback occurs instantaneously. This is why I said we’re in the upper right corner of the scatter plot. But what if we can’t act immediately and there are delays between measuring the output of the amplifier and computing the feedback signal? Rather than a nice and simple formula for amplifier gain, we get stuck with an equation that looks like

\(V_{\mathrm{out}}(t)= A \cdot V_{\mathrm{in}}(t) - A B \cdot V_{\mathrm{out}}(t-d)\)

This equation doesn’t have a clean analytic solution. Still, you can imagine what might happen: if Vin is changing at a rate comparable to the delay time, we might be effectively adding to the signal instead of subtracting. These errors can compound, and the signal might get amplified to arbitrarily high gains, ruining the amplifier. Control engineers are always wary of time delays and their pernicious effects, and the patches for dealing with them are quite complicated and non-elementary.

This simple amplifier example is instructive. By designing an actuator that acts instantaneously, the analysis becomes solving a simple equation. A barely quantified system can be made into a well-controlled, useful mechanism.  But there is no free lunch. Seemingly innocuous delays can bring the whole system off the rails.

Let me bring this back to decision making. The amplifier example is a bit contrived as we don’t think of electronic signal levels as “decisions.” But the ideas here generalize to a much wider set of general feedback rules. This general theory might be harder to explain in such clear terms, but let me attempt a summary in the next post.