Some of my best friends are statisticians.
Meehl's Philosophical Psychology, Lecture 6, part 2.
This post digs into Lecture 6 of Paul Meehl’s course “Philosophical Psychology.” You can watch the video here. Here’s the full table of contents of my blogging through the class.
“Some of my best friends are statisticians!” proclaims Paul Meehl midway through Lecture 6. Me too, Paul! Me too. And yet!
In the most epic rant of the quarter, Meehl lays out a complex argument about institutionalized statistics. On the one hand, he thinks statistics is necessary for science. On the other hand, he’s unconvinced that we need statisticians. Meehl complains that statistical culture harms inquiry.
“I am convinced—not only from my own sad experiences but other people's where I can be somewhat objective—that psychology editors should be very careful in sending articles that contain anything statistical to PhDs in statistics. Because they are a virulent, anal, rigid, dogmatic bunch of bastards, and they are in the habit of treating social scientists as if they were nincompoops.”
Meehl thinks this particular arrogant disposition arises from the statistician’s role as consultant. A scientific paper needs a stats section to be published. So statisticians set up clinics where grad students and faculty benevolently offer to help the statistically uninitiated with their designs and analyses. Meehl worries that a field considering themselves consultants reinforces bad associations with the role of the statistician and bad associations with social scientists more generally.
“There they are, Omniscient Jones in their office with their Gamma functions. And here comes poor little doctor Glotts, second-year resident in psychiatry, who hardly recognizes the standard deviation that he meets on the street. He's seen a few of these patients, and he brings in his little mess of crummy data and asks, “What do I do with this?”
“[Statisticians] get in a habit of talking to social scientists who are mathematically ignorant and pontificating to them. Consequently, if a psychologist or sociologist has an idea once in a while, he or she is likely to have trouble getting it published.”
Though Meehl is frustrated with statisticians and Statistics as a field, he is a proponent of statistical thinking. We’ll see this more over the remainder of the lectures. Meehl argues we use statistics because skepticism is essential in scientific thinking, and statistics can help formalize such skepticism.
“Science is a better enterprise from folklore and various other forms of human cognition because it has a set of procedures. One of its procedural things is ‘show me [because] I'm hard to convince.’”
Meehl is making a normative claim here that I don’t necessarily want to cosign. But let me try to unpack what he thinks is important. For Meehl, a core part of scientific thinking is collecting data and “finding out whether other people can see what you see.” Hence other scientists should approach findings with skepticism. Through an iterative debate in a field, perhaps some progress can be made. Meehl argues this is why we have “p<0.05.” The p-value was invented by Fisher—and motivated by statisticians before him—as a formal mechanism of skepticism.
But herein lies the challenge of statistics. Goodhart’s Law tells us that formalized rules of skepticism cease to be useful tools for the skeptic. Anyone who has looked at the current state of applied statistics knows we are in a mess. Even the simplest application of p-values confuses people and invites high-handed scolding from statistical clerics. We get endless meta-papers analyzing p-value distributions and tut-tutting about how they have the wrong shape.
At the other extreme, we have a finite suite of statistical tools accepted as canon that encourage the laziest, least motivated mathematical modeling. The idea that every analysis has to be shoehorned into a particular statistical formalization is ridiculous. We have a set of accepted analyses that make odd linearity, independence, and odds assumptions. Go read a few David Freedman articles, and you will quickly realize that none of these canonical statistical models are ever justified or validated. No one actually believes a time series model has the form
But we use run least squares on equations like this, make tables with asterisks, and declare causality because people have accepted Differences-in-Differences into the statistical canon (IYKYK). Such models are not just wrong, they are not even wrong. They are an incredibly fancy way of presenting correlational data to tell imaginary folk tales about causality. We accept this bizarrely limited modeling suite because it makes it easier to write and reject papers. But it doesn’t help us be more skeptical. If anything, it makes it easier to obfuscate results behind ornate statistical tapestry in a hundred-page appendix of robustness checks.
And this is my issue. A statistical canon just becomes a ritualistic set of rules required for paper formatting. Not a tool for overcoming skepticism. I think of statistical models the same way I think of plots. They have become a form of data presentation, not analysis. Forcing everyone to use a fixed set of statistical modeling rules is the same as forcing everyone to use the same visualization package. It’s like how in the New England Journal of Medicine, every paper has a Table 1 and a Table 2, and you know exactly what’s going to be in them. Applied statistics has become nothing more than an arcane rigid set of rules for how you are allowed to arrange your data in a paper. They have become rules of style, not instruments of discovery. But we imbue them with some sort of epistemological magic.
The problem is, no one is convinced by “p<0.05” anymore! We all now know that statistical sorcerers can make random fluctuations look statistically significant. Have we forced everyone to tie themselves to methodological rigidity that convinces no one of scientific validity?
People are obsessed with ways of making science more rigorous. One of my dear friends has an NSF IGERT on training people to do better science. But what exactly does that mean? Too often, rigor devolves into ritual. Preregistration and p-values. Robustness checks and Regressions. Are these achieving Meehl’s goal of convincing the skeptic? Remember how we got here in the first place! Meehl’s complaint was about loose derivation chains and bad modeling. Does tying our hands with rigid systems of rigor make these issues better or worse?
One thing is for certain: statistical rigidity inhibits creativity. In Lecture 6, Meehl is trying to feel out the balance between creativity and rigor in scientific investigation. It’s a real challenge. Let’s talk about that next and see if there’s a middle ground.


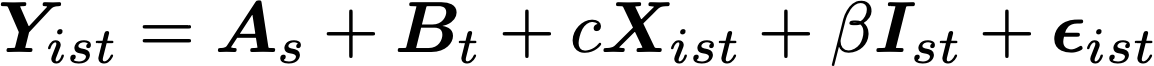
I highly recommend that everyone reading my post here should get familiar with the work of Professor Deborah Mayo. She is a genius in my opinion — her three texts written since 1996 are gems. Both are lucid but detailed and highly articulate; her writing addresses the present state of affairs vis-a-vis statistical hypothesis evaluation and scientific research. Start with her 1996 book, “Error and the Growth of Experimental Knowledge”. You will be rewarded.
The points here are bizarre at worst and at best simply out of touch with current statistical and social science practice. The criticisms of over-reliance on p-values, linear models, Diff-in-Diffs, etc are all 100% correct....if you stopped keeping up-to-date circa 2005.
Economics and political science-- two heavy consumers and producers of statistical methodology--have greatly advanced the state of art and science and practice of statistics. Just skim the writings of Andrew Gelman (Columbia) or Guido Imbens and Susan Athey (Stanford).