Overfitting to theories of overfitting
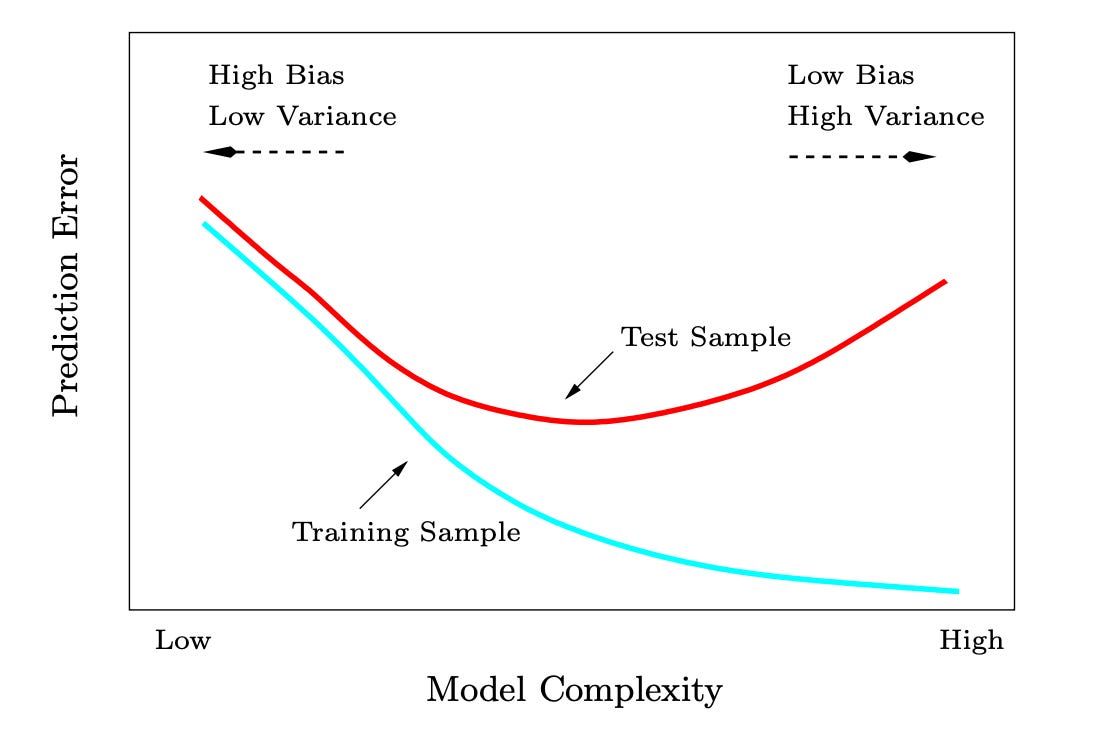
On a plot that radicalized me like no other.
I ended yesterday’s post arguing that we should remove this from machine learning classes.
This point was the primary source of negative feedback. I’ll bite the bullet today and try to explain why I think this plot is “not even wrong.” It is a meme that creates nothing but confusion
In case you don’t know, this plot comes from chapter 2 of Hastie, Tibshirani, and Freedman’s Elements of Statistical Learning. Let me be clear: this post and my related posts are an attack on the content of the ESL book, not the authors. Indeed, I know that Trevor Hastie has written papers arguing against much of what he wrote in ESL. For 2009, this book was probably not a bad thing. For 2025, there is ample evidence we need to teach this subject differently.
To understand the plot, let’s first define the used terms. The y-axis of this graph is prediction error, which means the average error of the function on a sample. That’s the only concept that’s well defined in this graph. What is model complexity? As far as I can tell, it means whatever you want it to mean.
ESL certainly doesn’t tell us. The book asserts, “More generally, as the model complexity of our procedure is increased, the variance tends to increase and the squared bias tends to decreases.” What are bias and variance? These terms are well defined, but only in a specific context.
I apologize for my non-theory readers, but I have to lean into math to define bias and variance precisely. First, we must measure prediction error in the square loss. Second, we have to believe the statistical learning gospel that data is generated iid from a distribution. With these two, we can write out a bias-variance decomposition. For any function fitting procedure, P, let fP be the function this procedure fits to a random training set. fP is a random function, where the randomness comes from sampling a training set. This means the prediction function has an expected value:
With this definition, we have the following decomposition:
Here the expected value is over the testing data and the training data. The first term is the irreducible error you’d get if you used the regression function
The bias is the L2-squared distance between fP and the regression function:
The variance is the expected value of the distance of fP from its expected value:
This bias-variance decomposition is always true for the squared loss. It’s just defining things in a clever way where when you expand the squares, the cross terms cancel because expressions have zero mean. The way the decomposition is interpreted in ESL is that more complex models have lower “bias” because they can fit more complex patterns but more “variance” because they are more sensitive to changes in data.
However, this decomposition is not a tradeoff because there is nothing that suggests these terms need to trade off. No fundamental law of functional analysis says that if one term is small, the other is large. In fact, there’s nothing that prevents both terms from being zero. I can certainly build models where some have low bias and high variance, some have high variance and low bias, and some are just right. It all depends on how you define the models and their complexity.
Wait, what is model complexity? As far as I can tell, it’s whatever you put on the x-axis of that plot. If you look at Chapter 7 in ESL, you’ll see that model complexity means a lot of things. In k-nearest-neighbors, it’s k. The smaller k, the more complex the model is. In linear regression, they claim the model complexity is “directly related” to the number of parameters. But this is already a great example where the bias-variance tradeoff falls apart.
Let me give a fun example. Let’s just assume that we have a legitimate linear model that statisticians love
e is Gaussian noise. x is Gaussian data. And β is a set of coefficients that decays as 1/k. Assume there are tons of dimensions and very few data points. This is a model. It’s not real. But we’re playing on statisticians’ turf to prove a point.
Model complexity will be the number of components we use in our regression function. What does the squared loss look like? You can plot it. Here’s a plot for n=40 training examples. Model complexity will just be the number of parameters I’m using in the model:
Huh, so this looks like what you’d expect, right? It’s just like ESL told us. You even get infinite prediction error if you let the model grow too complex! The thing is, you can keep going. What happens if we include more coefficients than data points? Well, now we get this plot:
Whoops. The error starts going down again. The best model has less than 40 parameters, but the prediction error curve is definitely not monotonic. The bias-variance decomposition holds for this problem. There is no bias-variance tradeoff.
This is an example of double descent. This particular model was analyzed by Belkin, Hsu, and Xu. Mei and Montanari showed a more dramatic curve in nonlinear classification, where the best models have the most parameters:
But let us not, um, overfit, to double descent. The thing to take away from double descent is that you can see it. But you might not see it. Depending on how you define model complexity, you can see all sorts of things. For example, here’s a plot from Liang, Rakhlin, and Zhai showing multiple bumps as you increase the model size:
Curth, Jeffares, and van der Schaar show that depending on how you define model complexity, you can see a proper bias-variance tradeoff or double descent. If you just give me a finite list of models, I can define “model complexity” at random and see whatever curve I want to see.
The advice people draw from the bias-variance boogeyman is downright harmful. Models with lots of parameters can be good, even for tabular data. Boosting works, folks! Big neural nets generalize well. Don’t tell people that you need fewer parameters than data points. Don’t tell people that there is some spooky model complexity lurking around every corner.
Use a test set to select among the models that fit your training data well. It’s not that complicated.


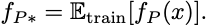








The graph looks intuitive to engineers like me since we are used to facing trade-off’s at almost every physical problem. For me, the bias-variance trade off appears as a parameter estimation problem in my mind: Given finite data, it is “more difficult” to reliably estimate many parameters than just a few parameters. Therefore, advice1: we should keep the number of parameters bounded. If we have very few parameters, we can reliably estimate them; but, the model will be crude and not useful with very few parameters. Hence, Advice2: have a lower bound on the number of parameters as well. The literature of AIC (Akaike’s information criterion), BIC on model order selection tries to do this selection systematically for us. These folks received awards for their works and it was our religion in engineering.
I believe our mental shortcoming stems from considering small data regime as the only possible regime of operation. The main issue especially in physical problems has almost always been making the best use of very limited data. The abundance of training data has lead to interpolation type results (with/without noise) and lead to this new school or church!
the easiest way to see the problem with this figure is being forced to teach it. students (in my class at least) would immediately see it was bs and ask the obvious questions about model complexity that you listed here. I was always left feeling deeply unsatisfied with teaching this lecture and the many after where we reasoned about whether the bias or variance would increase / decrease if we adjusted some hyperparameter \lambda.
i wasn't using ESL btw, but ISL, since it was an undergrad course. i inherited the course and taught it for several years. luckily i will not teach that course again :p.