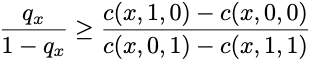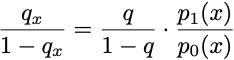Justify your answer
Three different views of optimal decisions
This is a live blog of Lecture 4 of the 2025 edition of my graduate machine learning class “Patterns, Predictions, and Actions.” A Table of Contents is here.
The simplest form of machine learning evaluation is binary prediction. Does a patient have a disease or not? Is there a star in this region of the sky or not? Is this transaction fraud or not? We label positive outcomes as 1 and negative outcomes as 0, with the definition of positive and negative left up to the application.
There are four outcomes of an individual prediction that we can assemble, each with some pre-enumerated cost. There is the cost of errors, when either you predict 0 when the outcome is 1 or predict 1 when the outcome is 0. There may also be a cost associated with a correct prediction. These costs can be negative, so you could consider receiving something for making correct predictions. I’ll write this as c(data, prediction, outcome) throughout. The first argument of the cost is the observed data, the second the prediction, and the final argument the outcome.
A quirky thing about the decision theory problem is that everyone stumbles upon the same optimal decision rule, regardless of how they model the future. If we let qx denote the fraction of the time the outcome is 1 in the future when the data is equal to x, then our best prediction is to predict a positive outcome when
and negative otherwise. The ratio on the left-hand side of this expression is called the “odds” for reasons I’ll explain in a minute. On the right-hand side of the inequality is a ratio of costs. The numerator is the excess cost accrued when you falsely predict an outcome will occur when it doesn’t. That is, the cost of a false positive minus the cost of a true negative. The denominator is complementary, measuring the excess cost of a false negative. This decision rule balances the cost of false positives against the cost of false negatives. When the cost of false positives increases, you need the outcome to be 1 more frequently.
There are three popular ways to arrive at this formula. Two use probability, the third envisions the prediction problem as a missing data problem. Let’s go through these:
The first probabilistic interpretation assumes that the outcome is random, with a particular propensity of occurring for each value of observed data. In this case, we can interpret qx as the conditional probability of a positive outcome when the data is x. With this interpretation, the left-hand side of the optimal decision rule is precisely the odds that the outcome is 1 when the data is x.
Under this model, we have a direct link between optimal decisions and gambling. The decision rule is telling us fair betting odds. The costs c(x,0,0) and c(x,1,1) can be payouts for bets, and c(x,1,0) and c(x,0,1) the cost of betting. If you are going to make a very large number of bets, you want to only take the bets where your model of the future says the odds exceed this particular ratio of costs.
The second probabilistic model flips things around. We now assume that a simple, biased coin flip determines the outcome, but the data presentation is complex and random. Some magical data-generating process first chooses an outcome by flipping a biased coin, equal to 1 with probability q. Then the data is sampled from one of two probability distributions. If the outcome is positive, the data is sampled from the density p1(x). When the outcome is negative, the data is sampled from the density p0(x). These distributions are called likelihoods. Using the definition of conditional probability, you can check that the odds ratio is proportional to a likelihood ratio:
Hence, if you know the frequency at which true outcomes occur and you have likelihood models, you can make optimal decisions by a likelihood ratio test: if the likelihood exceeds some value, predict a positive outcome. This form of decision theory is often called detection theory and was popularized in radar systems during the Cold War. When the probabilities of positive and negative events are equal, and the costs of errors are the same, the likelihood ratio test reduces to selecting the outcome with the largest likelihood. That is the well-known rule of maximum likelihood.
The likelihood ratio test highlights that optimal decision making partitions the space of data into two. There is X1, the set of all of the data configurations where our optimal decision is to predict 1, and its complement X0. The goal of machine learning and optimal decision making is to find a function that correctly assigns a positive value to all elements in X1 and a negative value to the elements of X0. In our probabilistic model, the log of the likelihood ratio (shifted by some constant) would serve as such a labeling function.
Now, in machine learning, we almost never have explicit probabilistic models of data and outcomes. In machine learning, prediction is a missing data problem. There is a population of outcomes on which we’ll be tested, and we want to find a prediction function that has low error when averaged over this population. As we saw last week, the optimal prediction rule still retains the same form as above. It just has a very different interpretation.
The gambler’s view imagines you are betting on an outcome and want to make sure the odds are in your favor. The RADAR operator’s view is one of statistical testing, deciding whether or not they believe they can reject a null hypothesis. The machine learning view is one of leaderboard maxxing, finding a decision that guesses the answers correctly in the hidden validation set of a Kaggle competition. These are very different models of the future! And yet, all three perspectives decide to use the same rule for optimal decisions.