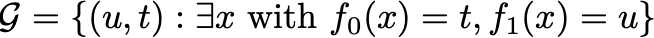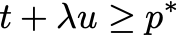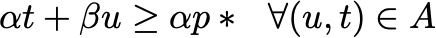Ends in a draw
A geometric argument for strong duality
This is the live blog of Lecture 10 of my graduate class “Convex Optimization.” A Table of Contents is here.
Last week, I showed how weak duality is an almost tautological condition. But convex problems also (for the most part) have strong duality, where the optimal value of the dual problem is equal to the optimal value of the primal problem. There are many different intuitions for why strong duality holds for convex problems, but the argument I like the most (and the one in Boyd and Vandenberghe) leans on separating hyperplanes.
Today’s blog has more notation than I’d like. Duality, it seems, is hard to motivate without getting technical! But my goal is to set up two pictures that illustrate why we should expect strong duality for convex problems and not nonconvex ones. Hopefully, those illustrations provide some intuition.
Let’s focus on a simple optimization problem today
Let p* denote the optimal value of this problem. To prove strong duality for this problem, we want to show that there is some value of the Lagrange multiplier, 𝜆, such that the Lagrangian provides an upper bound of the optimal solution
Let’s think about what this condition says geometrically. Consider the graph of the optimization problem
Then strong duality holds if we can find a 𝜆 where
For all (u,t) in the graph with u nonpositive.
This means we are trying to find a hyperplane that contains the graph of the optimization problem. Since we are looking at a problem with half spaces, we should turn the graph into a convex set. Let me define an “epigraph” of the optimization problem:
The desired strong duality condition amounts to a hyperplane that supports A at (0,t) and is sloping downward as in this picture:
Stare at the picture until you convince yourself it is the right condition. I always have to wrap my head around the mapping from the declarative form of the optimization into this geometric object. From this geometric view, the optimization problem is equivalent to minimizing the value of t in A with u=0. That is
The dual problem is maximizing the t-intercept of hyperplanes containing A. Indeed, for any value of 𝜆, the dual function value is the t-intercept of the associated hyperplane.
A picture also shows us what might prevent strong duality in the case of nonconvex functions.
Here, the t-intercept can’t reach the optimal primal value as it’s blocked by the nonconvex geometry.
These pictures suggest a path to verifying strong duality by showing there is a supporting hyperplane at the point (0,p*). To do this, define another set
A and B don’t intersect, so there is always a separating hyperplane
By the definition of A, 𝜶 and β both have to be nonnegative or else the affine function they define would be unbounded below on A. If 𝜶 is positive, then we can set 𝜆 = β/𝜶, and we will have proven strong duality.
To guarantee that 𝜶 is positive, you have to assume some extra facts about the optimization problem. These assumptions are called constraint qualifications. The only two most people need to know are (a) linear programming has strong duality and (b) if there is a point with f_1(x) strictly less than zero, you have strong duality. The second condition is called Slater’s condition.
Geometrically, strong duality was almost inevitable for convex functions. The Lagrangian was a hyperplane in disguise. We turned a problem about a convex set into a problem about the hyperplanes that contain that set. The duality between convex sets and the half spaces containing them is the fundamental property of convexity that enables all convex optimization.