Does what does not kill you make you stronger?

Nietzsche was the first bro scientist

In the 1940s, Hans Selye proposed a General Adaptation Syndrome (GAS) to model a body’s response to environmental shocks. The syndrome has three stages. First, an “Alarm Reaction” occurs when a person experiences a novel stimulus.  A “Stage of Resistance” follows a long enough period of Alarm Reaction, and the person displays increased resilience against this particular stimulus. The Stage of Resistance is followed by a “Stage of Exhaustion,” where systemic damage builds up so much that a person starts to lose the resistance capabilities they have developed.

Here’s a picture from Selye illustrating the ability to resist a stimulus over time.

The key observation here is that the body manifests a dynamic response to stimuli, and after an initial shock, it overcompensates and comes back more able to resist the stimulus. Seyle’s insight was that the body’s responses to all sorts of stressors, including injury, disease, or activity, were similar and could be studied in a unified framework.

In the context of exercise, this meant that we could consider many different modes of training with a single model. What are some examples of stimulus in exercise? The stimulus could be lifting weights. Lifting a weight makes you tired and sore. It could be running on a treadmill. 

You get out of breath after running. But even though these exercises make you tired in different ways, GAS conceptualized the responses to training as similar. We could think about training strategies for either a triathlon or a powerlifting meet with the same framework.

What does GAS suggest we do to train? It’s sort of obvious from the picture: introduce enough of a stimulus to induce an adaptation (so the curve goes negative and then positive) but also allow rest periods to prevent injury and exhaustion. Repeat this process enough times, and next thing you know you’re faster than Usain Bolt.

But how much stimulus should we introduce? How must rest should we take? Selye’s qualitative model didn’t answer this.

In the mid-1970s, researchers built more quantitative models of adaptation in the context of exercise. Calvert and Banister introduced a fitness-fatigue model that captured much of the qualitative aspects of GAS but could make some rudimentary quantitative suggestions.

The fitness-fatigue model posits that the body has two competing systems, a system of positive adaptation and a system of exhaustion. The simplest model for this is to assume both are first-order systems:

fitness[later] = A*fitness[now] + B*stimulus[now]

fatigue[later] = C*fatigue[now] - D*stimulus[now]

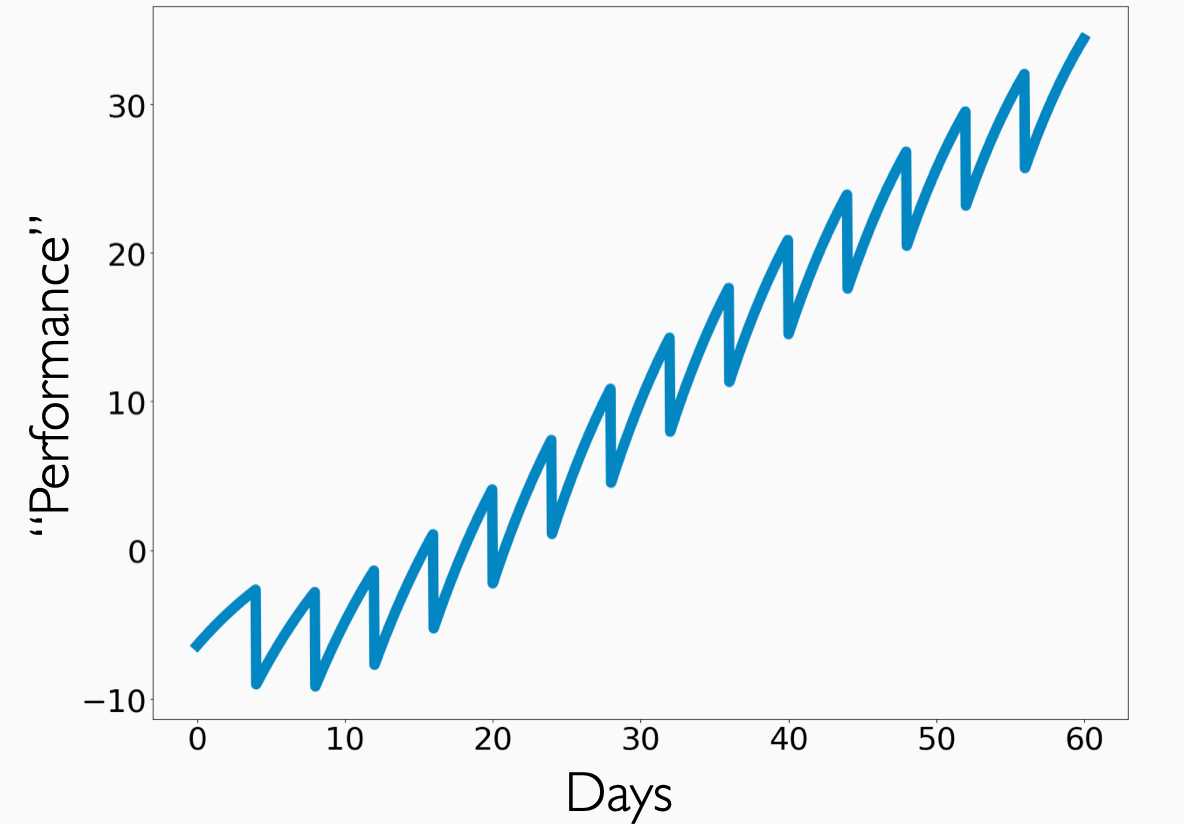
(That is, the model says hear me now and believe me later.) Performance is equal to the sum of fitness and fatigue. Here A, B, C, and D are all positive numbers that depend on the individual person. The response to a stimulus would then look something like

Now, if you introduce a stimulus over time, these things stack together:

And over the long run, the model predicts an outcome like this:

The simple model captures some qualitative features that are familiar to anyone who’s taken an exercise class. Initially, you get sore and tired and frustrated. But after that initial hazing period, you start to pick up the skill you’re chasing and rapidly improve. The rapid improvement eventually slows, and your performance plateaus, but you still eke out more improvement over time if you keep at it.

One prediction of this model, which perhaps is not obvious, is that tapering training before a competition may lead to an extra bump in performance. Professional athletes all do this, but the model of adaptation explains why it’s a good practice: The “fitness” component decays more slowly than the “fatigue” component. 

This simple model of adaptation is impressive in the qualitative suggestions it makes, even without concrete values for the dynamical system parameters. For my control theory friends who are still reading this, the fitness-fatigue model provides a class of dynamical systems where every model in the class has a similar optimal control policy. Moreover, it is unclear how much we need to identify each system to steer it to optimal performance. A simple PID-like control policy (train harder than last time, just shy of failure), works no matter what the system parameters are. This control policy is what exercise scientists and gym bros call “Progressive Overload.”

The problem with the simple fitness-fatigue model, of course, is it is looking at performance as a singular metric that you want to optimize. Is it that simple? In a 100m dash, if all you have to do is get faster, does that mean you should just run the 100m dash every day with some appropriate rest? No, it’s not that simple. And certainly, it’s not the case that for a tennis player that the stimulus of “more tennis” is going to follow this simple model of Calvert and Bannister. Progressive Overload is the first step to target very specific systems. But to train an athlete to be resilient to multiple sources of stress, we need periodization. I’ll dive into this next time.