Cone Programming
Sometimes a technical term makes for a catchy title.
This is the second part of the live blog of Lecture 7 of my graduate class “Convex Optimization.” A Table of Contents is here.
At least once a semester, I end up with a lecture where I only get through half of what I had planned. It’s always worth reflecting on what made this content particularly challenging, so as a note to my future self, I’m just going to write what I had intended to lecture about in today’s post. Next time I’ll remember to split this over two lectures. Today will be closer to traditional lecture notes with too many mathematical formulas. I apologize in advance to all of you reading.
Minimization over cones
A convex cone is a set where arbitrary nonnegative linear combinations of the points in the set lie in the set. The canonical example we’ve already encountered is the cone of nonnegative vectors, the nonnegative orthant. Any nonnegative linear combination of nonnegative vectors is a nonnegative vector. Two other cones show up a lot in optimization: the second-order cone
and the positive semidefinite cone (the set of all positive semidefinite matrices).
These cones are central to optimization because their geometry makes it easy to verify optimality.
Optimality conditions over cones and dual cones.
How do you check if a point x minimizes f(x) over K? It is necessary and sufficient that
This formula says that the directional derivative of f in all directions that stay feasible in K is nonnegative. That makes sense as an optimality condition! I’ll prove it in full generality on Tuesday. When K is a cone, this formula simplifies to the following check: x minimizes f over K if
Where K* is the dual cone of K:
K* is itself a cone (it is closed under nonnegative combinations). Verifying optimality in a cone program amounts to testing if a point is in a dual cone.
The wild part about the three cones I introduced above is they are self-dual. The set of vectors whose dot product is nonnegative with every nonnegative vector is the set of nonnegative vectors. You can check the same holds for the other two cones too (Verifying this in class turned out to require more algebra than I had anticipated. Sigh). You can also check that any cartesian product of self-dual cones is self-dual. That is, the cone
Is self-dual if K1 and K2 are.
If you have a cone where you can do local search, you can also verify local search has converged. That’s half of why I wanted to introduce the self-dual cones today. The other half is because you can pose 90% of the problems in the book as a linearly constrained cone program
where K is a Cartesian product of orthants, second-order cones, and positive semidefinite cones.
Cone programming
It took me too long to get to this point, so I ended up rushing all of the examples. But let me list them here, and you can check the relevant sections in the book for full details.
First, see Section 4.4.2 with regards to second order cones. Any convex quadratic constraint can be posed as a second-order cone constraint. Convex quadratic programming is a special case of second-order cone programming. I made this so much more complicated in class than it needed to be! If you were confused, check out Section 4.4.2.
SOCPs also come up in robust linear programming. This discussion consumed more time than I had anticipated, but I think it was worth it in retrospect. I’ll add a whole lecture on robust optimization in the second third of the class.
Stochastic programming is a bit confusing. We want to devise a policy where we model the constraint as a random variable that we don’t get to see until after we declare our policy. We also assume our policy has no impact on the randomness. This lets us pose a chance constrained problem
where the randomness only lies in the vector a. We choose x so that whatever a ends up being, the constraint is satisfied with high probability. It turns out that for an appropriate choice of uncertainty set U, this problem is equivalent to the robust linear program
This problem is a linear program with an infinite set of constraints. There is a constraint for every a in U. But it captures what the stochastic problem was after. A probabilistic constraint asks about the worst possible occurrence in a confidence set. U is the appropriate confidence set. In the case that the probability is Gaussian, the confidence set is an ellipse, and both problems can be posed as second-order cone programs. 4.4.2 has all the gory details!
I ran out of time before I could discuss semidefinite programs. I was going to work through the matrix norm minimization problem from Section 4.6.3. Take a look and see if it makes sense! In particular, I wanted to work through some manipulations of Schur complements. This is a super useful manipulation that turns very nonconvex looking problems into SDPs. Those tricks will have to wait until after we cover duality, but you can see them in Section 4.6.3.
The part I’m most disappointed about is I didn’t get to explain that LPs and SOCPs are special cases of SDPs. Any Cartesian product of orthants, second-order cones, and positive definite cones can be embedded in a large semidefinite cone.
If x is a nonnegative n-vector then diag(x) (the n x n matrix that has x on the diagonal) is positive semidefinite. If (x,t) is in the second-order cone, then
In this sense, SDPs are the master problem for understanding the sorts of constraints over which we can tractably optimize. You might argue with what I mean by “tractable” when we try to implement SDP solvers. However, as a theoretical construction, understanding the inevitability of semidefinite programming is fundamental to understanding the state of convex optimization.









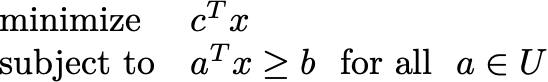

Curious if you are planning cover something that would work to minimize over space of orthogonal matrices. Currently trying to get a more efficient way of maximizing Tr(W) subject to WW'=I and WX=Y constrains