Basic Linear Algebra Subprogramming
The hidden technology under the hood of numerical optimization
This is the live blog of Lecture 16 of my graduate class “Convex Optimization.” A Table of Contents is here.
Even though this class focuses on modeling, it’s helpful to understand a little bit about how to solve convex optimization problems. Many people can avoid ever looking across the abstraction boundaries. It’s likely possible to get a feel for the optimal use of tools like cvxpy without digging too much into how they work. Whether using Stata to solve regressions or pytorch to fit neural networks, you can learn heuristics for speedups without knowing what’s under the hood.
Unfortunately, the sad part of computational mathematics is computers are never fast enough. We need to pose problems that are solvable on the compute to which we have access. If you don’t have billions of dollars of Azure credits, then you have to understand a bit about what your solver does to get a solution in a reasonable amount of time. Solver knowledge can save you a lot of trial and error and reliance on folklore. A little bit can take you a long way.
In this class, I’ll focus on the solvers that try to solve optimality conditions. Gradient-based solvers are the best-known example. For unconstrained convex problems, the gradient vanishes at the optimal solution. So to minimize a function f, our goal is to find a point where
This is solving a nonlinear equation.
For constrained optimization, the KKT conditions generalize the gradient condition. They are a set of equations that are necessary and sufficient for optimality, a combination of nonlinear equations (the gradient of the Lagrangian must equal zero, the equality constraints must be satisfied, and complementary slackness must hold) and constraints on the nonnegativity of variables. Convex solvers try to solve these nonlinear equations subject to holding variables being nonnegative.
Nonlinear equations don’t typically have nice closed form solutions. To be fair, we learn in high school that linear equations don’t have simple solutions either. We have to slog through Gaussian elimination to solve systems of three equations in three variables. Nonlinear equations are worse, however, as there are no natural analogs of Gaussian elimination.
Instead, we solve nonlinear equations by sequentially solving linear equations. The most famous example of solving nonlinear equations by linear equations is called Newton’s method. Let’s say you want to solve a nonlinear system of equations F(x) = 0, which has n variables and n equations. That is, F has an n-dimensional vector as input and an n-dimensional vector as output. Newton’s method iteratively solves a linear approximation to this equation. Suppose your current approximation is x0. You can make a Taylor approximation to F as
Since F maps n-vectors to n-vectors, the “gradient” here is an n by n matrix called the Jacobian of F. If we set the Taylor approximation equal to zero, we get the update
where v is the solution to the linear equation
Under reasonable conditions, iterating this procedure will find the optimal x.
I’ll talk more about Newton’s method in the coming lectures, but I wanted to at least introduce it today to show why we care so much about solving systems of linear equations. The backbone of optimization methods is the solution of linear equations.
Since the dawn of the computer, we’ve optimized our architectures to solve linear equations. Linear systems solvers are built upon optimized computational primitives that let the end user type “A\b” or “np.linalg.solve(A,b),” and then you don’t have to worry about what’s under the hood. If you can reduce your optimization problem to a few of these API calls, you should consider this a win. You can lean on some of the most optimized numerical software in existence.
Except, as I’ve been saying, it’s not quite that easy. Algorithms for linear equation solving run in “polynomial time,” but the associated scaling may still be prohibitive. Adding two n-vectors together requires approximately n arithmetic operations (or FLOPs, if you prefer). An algorithm that requires a constant multiple of n operations runs in linear time. Multiplying an n x n matrix times a vector requires approximately 2n2 arithmetic operations. Algorithms that require a constant multiple of n2 operations run in quadratic time. Solving Ax=b for general matrices requires on the order of n3 operations, called cubic time. For large systems, cubic time algorithms are prohibitively expensive.
It’s thus important for a modeler to understand how computers solve these systems. You want to build models that lean on the strengths of your solvers. If I tell you that arranging your model in a particular order can buy you a factor of 10 speedup, I’m sure you’ll take it. You might never implement a linear system solver, but you should know which models the solvers are best suited for.
Hence, our tour of convex optimization solvers starts with a tour of linear system solvers. Some problems can be solved in linear time. The simplest are diagonal systems. If A is a diagonal matrix, then you can solve for each coordinate independently. This requires only n arithmetic operations. Other more complicated matrix forms also admit linear time solutions. A notable example is the tridiagonal system, where the matrix A is only nonzero on entries just above and below the matrix diagonal.
A step up in complexity is quadratic time. If a matrix is orthogonal, so that A-1 = AT, then you can invert it by a matrix multiply in quadratic time. If a matrix is lower triangular or upper triangular, substitution algorithms solve the associated systems in quadratic time.
Linear systems solvers try to factor the matrix A into a product of matrices where equation solving is at worst quadratic time. With such a factorization, you can solve your system in quadratic time. Most of the cost in modern linear systems solving is thus in matrix factorization. Today’s lecture will take a tour of the most common factorization techniques.


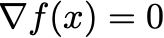
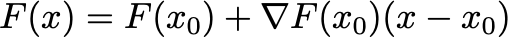
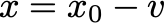
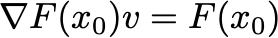
"You want to build models that lean on the strengths of your solvers"
If you put it on a shirt, I'll buy it.