Apostasy or reformation

Inductive bias just means I don't understand

Feeling like I’m already a relic of history, let’s start our qualitative tour of machine learning practice revisiting Rethinking Generalization. This paper was a beginning of an end for me.

Before 2015, I believed a list of truths about machine learning:

1. Good prediction balances bias and variance.

2. You should not perfectly fit your training data as some in-sample errors can reduce out-of-sample error.

3. High-capacity models don’t generalize.

4. Optimizing to high precision harms generalization.

5. Nonconvex optimization is hard in machine learning.

None of these are true. Or certainly, none are universal truths. What changed my mind? And can I still change your mind?

While both of us were at Google, Moritz Hardt and I arrogantly and naively schemed to write some theory papers making sense of deep learning. We had a few conversations with Oriol Vinyals, and he told us things that sounded crazy. People didn’t worry about training error. You could just get it to zero. People would pick models based on appropriate intuitions and choose the ones that would train quickly on the custom cloud computing stack Google had built for deep learning. Oriol also said that depth wasn’t really a difficulty impediment. Sometimes deeper models were easier to fit than shallow ones.

I didn’t really get what Oriol was saying, so I tried to re-implement some of the deep models for myself. This was an exercise to learn TensorFlow, which was in late beta stages when I arrived [insert Grandpa Simpson meme]. I reimplemented the famous “AlexNet” architecture, and lo and behold, if you just turned off the “regularizers” the training error went to zero. And this was quite repeatable on all of the “small” datasets like CIFAR10 and MNIST. Getting the training error of deep models to zero was easy.

But perhaps the surprising part wasn’t just that the errors went to zero, but the test error didn’t go to random chance. My recreated AlexNet model got 18% error (with no data augmentation). When I turned off the regularizers, the test error went up to 23%. So the regularization parameters were certainly doing something, but they didn’t seem too different from any other hyperparameter. They were just knobs I could turn to get the error down, but not some essential key to test-set generalization.

Moritz and I decided we should dig deeper into this, and we convinced Chiyuan Zhang, who was interning at Google, to join us. Chiyuan was a wizard and started running dozens of experiments. Every time we’d meet and decide to try something crazier, he’d figure out a way to get the Google architecture to make it happen.

On CIFAR10, Chiyuan tried more sophisticated models than AlexNet. On Google’s “Inception” architecture, again with no regularizers, the error now dropped to 14%. On a ResNet, the error was 13%. The most hyper-regularized Alexnet was 5% worse than unregularized models that had more than ten times the number of parameters. Something was broken.

Perhaps this was just a pathology of CIFAR10. CIFAR10 is a weird set of thumbnails that are not particularly easy for anyone to classify. We turned to a bigger fish: ImageNet. ImageNet was what put deep learning officially on the map. Imagenet was real images. Just look at the difference between CIFAR10 images and Imagenet images:

ImageNet had over a million training examples. Everyone thought this was a hard learning problem. We all figured we wouldn’t be able to find a model that interpolated this data and still worked well.

Whoops, we were wrong. 

With Google’s in-house Inception v3 model (again without data augmentation), the Top-1 training error increased from 30% to 40% when we turned off the regularizers. 40% sounds bad, but 40% Top-1 error was still better than any non-neural model ever fit to this data set. In fact, the original Alexnet paper of 2012 only got 36% top-1 error, using both regularization and data augmentation.

The thing that was crazy is that we these particular parameter settings, we could fit anything we wanted. Without changing any of the learning rates, we could fit completely random label patterns on Imagenet. The model had enough capacity to fit any training pattern. From a capacity perspective, it was no different than a radial basis function. So why did Inception get top-class performance whereas an RBF wasn’t much better than random guessing?

I have no idea, and I still have no idea. It’s certainly true that whatever model we’re converging to has some remarkable properties. It is certainly not the case that all architectures get the same out-of-sample error. But, on ImageNet, what makes for a good out-of-sample error seems to be a lot of local iteration from conv nets. Intuition from signal processing might help. But I don’t think anyone has convincing explanations for why any particular architecture works better than any others.

What we do know is that architectures that are good on ImageNet are usually good on other data sets too. There is a lot of transferability. That provided a way forward. First, hack on CIFAR10. If whatever you’re doing works on CIFAR10, try it on ImageNet. if it works on ImageNet, adapt it to the specific problem you actually care about. Machine Learning runs a large-scale genetic algorithm through competition amongst ambitious hackers looking to get promoted and big tech companies who want to outdo each other with bullshit generators in all of their products.

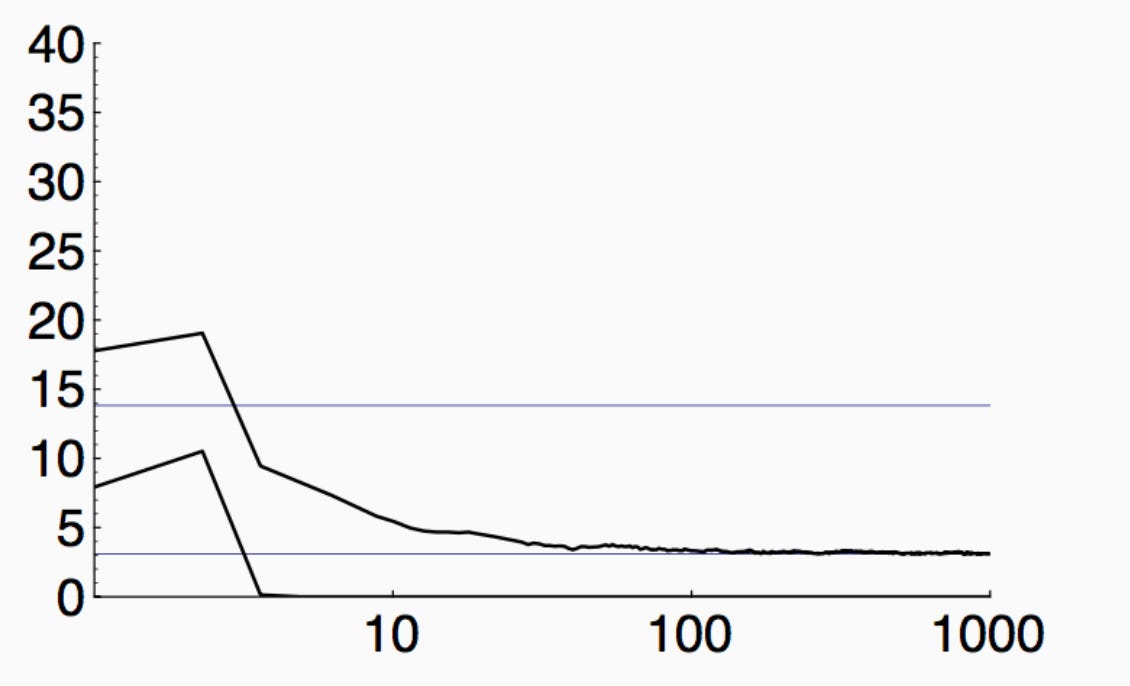
The thing is, I’ve mentioned this before, but we have had plenty of evidence before deep learning that the religious rules I began this blog with aren’t true. Boosting advocates noted in the 1990s that boosting performance kept getting better well after the training error was zero. Here’s a plot from a 1998 NeurIPS tutorial by Peter Bartlett, the bottom curve being boosting train error, the top curve boosting test error:

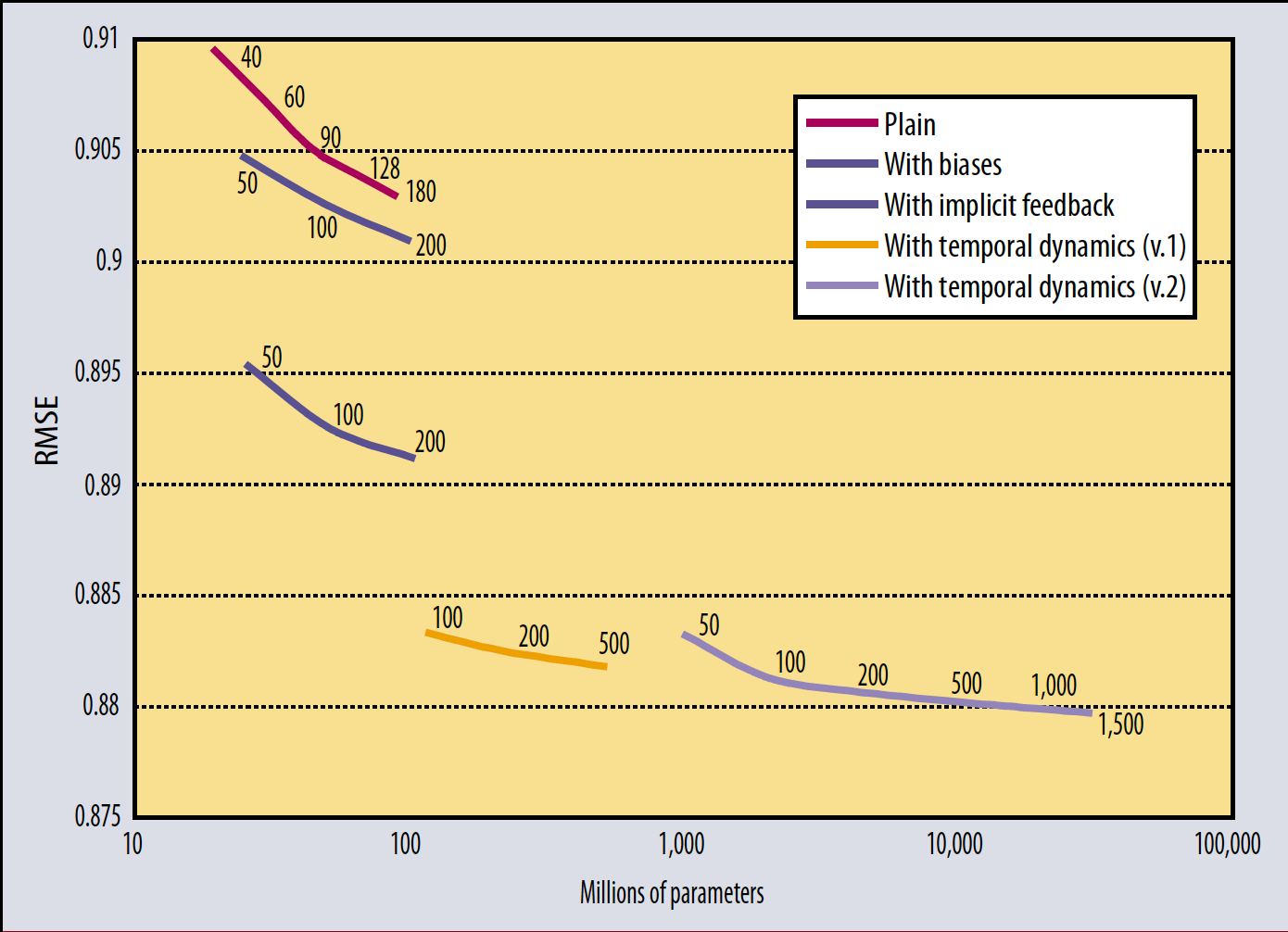
And in the Netflix Prize, the first big public machine learning leaderboard competition, here’s a plot from Bell and Koren on how the more parameters they added to their model, the better their performance was.

Given all of this evidence, why did we teach our undergrads a paradigm completely invalidated by empirical evidence? I don’t have an answer to that question.

What I do hope to be able to look into is the robustness of this train-test paradigm. Another religious belief we used to teach our undergrads is that you can never evaluate test error. That the test error is a sacred box to be inspected only once. We taught that if you violated this sacrament, you were cursed by “test-set leakage” which would destroy performance on new data. This conventional wisdom is also completely false. Why? Next week, we’ll dive into competitive testing and try to understand how the test set truly functions in machine learning practice.