All paths point downhill
Design primitives for optimization methods
This is the live blog of Lecture 17 of my graduate class “Convex Optimization.” A Table of Contents is here.
Our first lecture on optimization algorithms focuses on the unconstrained problem with no constraints. We have a function that maps arrays to real numbers, and our goal is to find a configuration of the array that makes the function as small as possible. There are several ways to approach this problem, but most algorithms can be derived using one of three designs.
The first algorithmic idea is the most intuitive: local search. Given a particular assignment of the variables in the problem, we can look for small tweaks to make the function value a little bit smaller. By chaining such moves together, we should eventually reach a point where we can’t make the objective any smaller.
The second idea is global optimization. We specify a property that certifies we have a minimal objective value and then try to find a variable assignment that satisfies this property directly.
The third idea lies in between the first two. We approximate our objective function by a function that is easy to minimize (say, a quadratic function). If the resulting solution isn’t good enough, we can repeat this approximation process.
In unconstrained optimization, almost every algorithm we have developed is interpretable in all three ways. These apparently different high-level ideas all lead to the same algorithms.
Let me prove my case by starting with the method everyone loves these days: gradient descent. I am told this algorithm will solve general intelligence if you set the optimization problem up correctly. We live in an age of miracles and wonders.
Gradient descent is motivated as an obvious local search heuristic. The negative gradient gives the direction that most decreases an objective function. Following this move makes the most local improvement. We can also think of gradient descent as a global method. If we want a point where
We can solve a fixed-point equation
where s is a positive real number. If the mapping from
is a contraction mapping, then iterating by the rule
yields a fixed point. In this way, gradient descent is an equation solver. What about as an approximation method? Well, by judiciously picking a scalar s, we can write a Taylor expansion of our objective function
Minimizing this expression also gives the gradient descent step.
In this class, Newton’s method will play a more central role than gradient descent. Newton’s method tends to converge in fewer iterations than the gradient method, but each iteration requires more computation. Newton’s method also has the same three interpretations. Usually, Newton’s method is motivated more generally as equation solving. For any nonlinear set of equations
We can approximate this as
Setting the approximation equal to zero gives us
In the case of trying to solve for a point where the gradient of f equals zero, this iteration is
This is Newton’s method, derived as a global optimization algorithm. However, this iteration is also the solution of a successive approximation to f. We could have written a Taylor expansion
Minimizing this expression gives us the step of Newton’s method.
Similarly, Newton’s method is a descent method. To understand why, remember that a direction decreases a function value if its dot product with the gradient is negative. Newton’s method moves in the direction:
For convex functions, that inverse Hessian matrix is positive definite. Hence, the dot product between the Newton direction and the gradient is a negative number. That is, Newton’s method moves in a direction that locally decreases the cost function.
We can derive similar arguments for other popular algorithms like proximal point methods, BFGS, or nonlinear conjugate gradient. So why are local search and global optimization so tightly linked? It’s because we derive optimality conditions by thinking about local search. We say that x is locally optimal if f(z)>f(x) for every possible z. In particular, this means that all local moves increase the objective function value. We can find a locally optimal x by either performing local search or by globally searching for points where local improvement isn’t possible.
To make this concrete, if the gradient of a differentiable function is equal to zero at x, then there are no local paths of improvement from x. We can either follow directions correlated with the gradient or solve the nonlinear equation seeking a point where the gradient equals zero. These end up doing the same thing.
Though we’d like to think we’re more clever, all roads lead back to naive local search. James Lee once told me that he thought that we only had two algorithmic ideas: gradient descent and dynamic programming. There are certainly exceptions, but it’s remarkable what problems we can solve with just these two primitives.





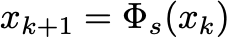
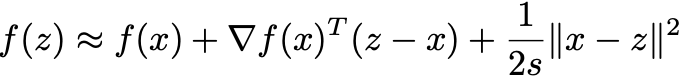
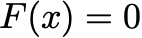





Thank you for resisting the urge to say "Gradient descent is all you need."