All models are wrong, but some are dangerous

Doyle's counterexample and the paradox of prediction in optimal control.

In the last blog, I argued that the ability to act rapidly and impactfully reduces our need for quality uncertainty quantification. Perhaps paradoxically, I’ll show you today how improving predictions can also harm your performance when you act rapidly. Why can’t we have nice things?

I first described this paradox in a series of blogs in the Summer of 2020 ([1] [2] [3]), using a classic counterexample in control theory. The blogs argued that optimizing performance under some model of the world made the optimizer very sensitive to modeling errors. And these sensitivities might arise in completely unexpected ways.

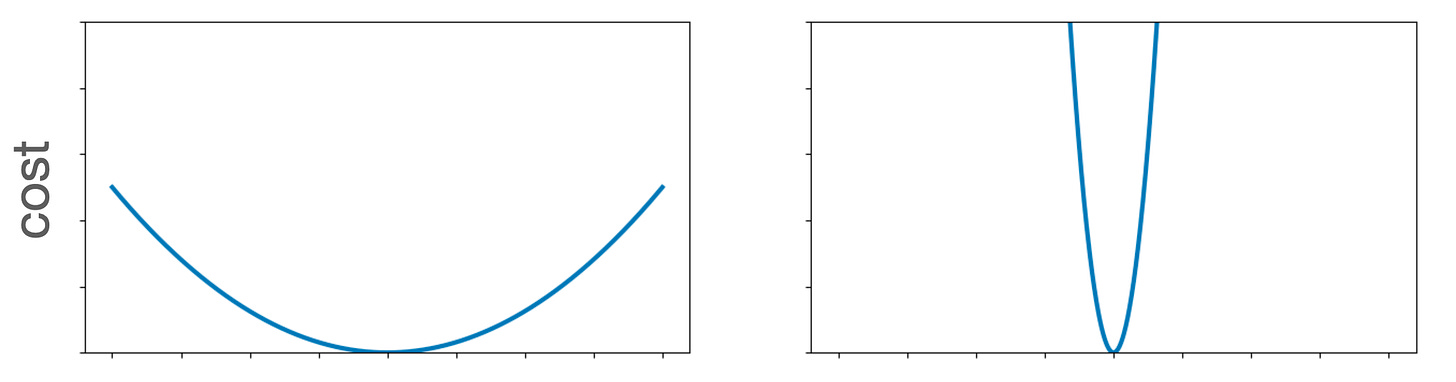
To understand what's happening at a high level, let’s leave feedback systems aside for a second and just think about pure optimization. For any optimization problem, there will be a bunch of policies near the optimum. Some of these nearby solutions should probably be close to optimal. How quickly these other candidate policies move from optimal to suboptimal depends on the specifics of the optimization problem. If the cost function looks like the function on the left, small deviations from an optimal policy are almost as good as the optimal policy. But nearby policies can be quite bad for the cost function on the right.

In high dimensions, the definition of “nearness” is more complicated.

In one direction of this two-dimensional cost surface, nearby policies yield nearly optimal cost. This is the dark ridge in the plot. In the orthogonal dimension, small perturbations to the optimal policy result in very high costs, illustrated by brighter colors. This is an example of an ill-conditioned optimization problem. For this problem, you can just look at the plot and know that you’d better be careful about certain deviations from the optimum. But ill-conditioning can creep up on you in many unforeseen ways.

And there are tons of weird ways where ill-conditioning pops up in optimal control. Optimal control takes a measurement of the state of the system and computes an appropriate action. When the control system can measure the state to infinite precision at every time step, the optimal control problem is robust to all sorts of perturbations. The first blog highlights some of the remarkable robustness, showing how over huge ranges of misspecifications, as long as you measure your state completely accurately, the system doesn’t crash.

But what happens when we bring prediction into the picture? Instead of knowing the state of the world, we try to predict it using machine learning. In the stockroom example that I ran with in the previous blog, I wanted to order just enough supply to cover tomorrow’s demand. Imagine I don’t wait until the end of the day to reorder but instead make an order in the morning based on my prediction of sales for the day. Can I still find a reasonable policy based on these predictions?

When we only have partial information about the state and need to use algorithms to predict it, the situation becomes surprisingly complicated. In the second 2020 blog, I described John Doyle’s famous “There Are None” counterexample, showing something that feels completely wrong. In Doyle’s example, improving state prediction makes the system less robust. Why? It’s because better measurements make a feedback system more fragile to modeling errors. In retrospect, perhaps this makes sense. A model might have certain signals it assumes are always equal to zero and certain signals it knows are critical to good performance. As the measurements improve, the control will focus on the signals needed for performance and use the fact that it doesn’t need good estimates of the signals the model assumes are zero. But if those signals are nonzero, the system is doomed. It ends up amplifying directions that it was told were equal to zero. These amplified control messages can drive everything off the rails because the designer assumed they were unimportant. Small model mismatches are enough to crash the system. Yikes!

Why is this happening? It’s a problem of ill-conditioning. The solution of the control problem has hidden directions that get large quickly. In optimal control, there are no 2D clean surface plots like those earlier in this post. The small model mismatches are the ill-conditioned directions, but a decade of control researchers didn’t see them.

This is super annoying. You make your measurements better (in ML land, perhaps by getting more data) and you become more vulnerable to your models being wrong.  I’m not sure any of us would imagine that a better prediction would lead to a worse policy. But I’ve spoken with people who have improved their machine learning systems only to see their profits fall. Caveat emptor. You can fix this by pretending your data is bad, or you can fix this by better understanding your broken model. 

Optimal control lets you specify complex models of reality, but catastrophe will ensue if you believe that model too much and it’s wrong. More broadly, when making decisions under uncertainty, you have to know which errors to account for. But finding those errors is not always obvious. Uncertainty quantification is not only a matter of quantifying the “known unknowns.” It’s about being ready to recover from unknown unknowns too. 

I suppose the robustness analysis in my 2020 blogs amounts to just doing some mathematical manipulation that would be straightforward for any skilled Ph.D. in control theory. But this isn’t a satisfying solution. If you want widespread, safety-critical systems, you can’t require Ph.D.s to tune every fine detail. (Here’s looking at you, AI bros). When can we get adequate performance that is robust but simple? Next week, I’ll try to explore some possibilities.