A game of chance to you to him is one of real skill

Reducing policy optimization to gambling

Action naturally puts us in the mindset of optimization. If we are picking between options, it feels reasonable that there should be some “best” course of action given the information we have on hand. Yesterday, we decided upon some probabilistic models of hidden states. Today, let’s formalize how we’d act upon knowing those states.

Surmising the situation and declaring an action is the prescription of a policy. A policy maps observations to actions. Our goal will be to find a policy that maximizes some particular desired outcome. The remainder of the semester will be focused on policy optimization in one way or another.

For each action, there will be some reward that is a function of an unknown condition of the world. If we knew the condition, we could just look at the associated rewards and pick the action with the highest return. The problem only becomes interesting when the cost is a function of some unknown condition, and we need to infer that unknown condition given the data on hand. We observe some measurement that provides some notion of the condition we’re interested in, but we don’t actually know the condition in advance. Hence, the need for a policy. Our goal will be to find the best action based on measurement, with uncertainty about the actual value of the condition governing our reward. 

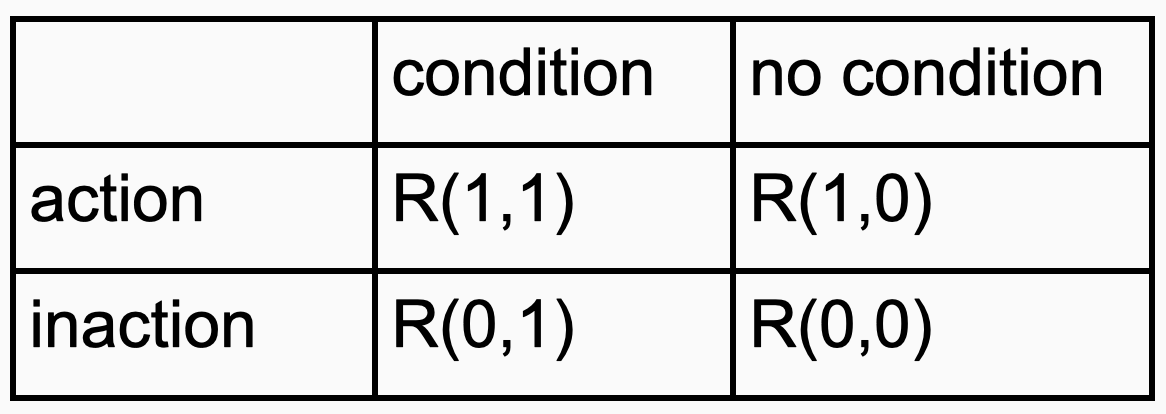
Today, we’ll consider the simplest version of the problem.  You either act or your don’t (do or do not, as Yoda preaches), and the condition either exists or does not. This means there are only four options to understand: What happens when we act and the condition is true? What happens when we don’t act and the condition is true? What happens when we act and the condition is false? What happens when we don’t act and the condition is false?

We can summarize the case of a single action and condition in a table of rewards:

Since the relationship between our measurement and the condition we care about is uncertain, we decided yesterday to model the outcome probabilistically. Then perhaps we can start by considering how to maximize the reward of a policy in expectation. We can weight the reward of associated with a measurement and condition by the probability of observing that pair. 

Mathematically, this means we’re solving the problem

\(\text{maximize}_{\pi}~~\mathbb{E}_{p(x,y)}[R(\pi(x),y)]\)

Here, π is the policy function we’re after. What this expectation means in reality is complicated philosophically, and I’ll discuss this more tomorrow. But for today, let’s solve the optimization problem and see where it takes us.

This problem turns out to have a simple solution. By construction, we are choosing an action for every measurement that could occur. And nothing in the formulation forces us to take similar actions for similar measurements. This means we can find the best action for each measurement individually. Working through an argument based on the law of total expectation, we find the optimal policy to be given by the pseudocode

if odds(condition given data) > (R(0, 0)-R(1,0))/(R(1, 1)-R(0, 1)):
     take action
else:
     don't take action

We need to be able to estimate the odds that the condition is present given our observations. Once we have determined these odds, our decision rule is determined by the relative rewards of taking actions under different conditions. 

The simplest example here is gambling in a casino. In this case, the rewards will be actual dollar amounts associated with bets. Ignoring appeals to behavioral economics, let’s just assert there is no cost or reward associated with not betting. So there are two cases: if you bet and you lose, you will lose -R(1,0) dollars. If you bet and win, you get R(1,1) dollars. This optimal decision rule tells you that you should bet if the odds of winning exceed R(1,0)/R(1,1). It’s the same as saying “only bet when you have a positive expected reward.” The casino setting is where expected reward maximization makes the most sense. Not for the gambler but for the casino. If the casino knows that the expected value of every game is negative for bettors, they will come away ahead as long as they entice enough people to play. Because these games are legitimately games of chance, they can choose games so the house always wins. The gambler is at the casino for reasons other than rational expectation maximization.

Other problems where we try to apply this framework of reward maximization are a little less cut and dry. My last two examples are easier to describe as minimizing expected cost rather than maximizing expected reward. The algorithm doesn’t change. Letting C denote the cost function, we find

if odds(condition given data) > (C(1, 0)-C(0,0))/(C(0, 1)-C(1, 1)):
     take action
else:
     don't take action

Mechanically and mathematically, minimization and maximization are equivalent. Maximizing a function is the same as minimizing the negative of that function. But, as Ben Van Roy often points out, maximization and minimization are philosophically quite different. Problems of minimization tend to focus on costs. In most formulations, costs are bounded below by zero. Zero cost is the ideal setting, and hence the goal is to end with worlds that are stable and robust. Maximization, on the other hand, is optimistic. In maximizing profit or pleasure, the goal is unbounded above. Hence we seek algorithms that are inherently aggressive and unstable. This dichotomy manifests itself in optimization practice. Choose wisely, I suppose.

Optimal decision theory originated in the design of radar systems during World War II. When a plane was on radar, there was some noisy signal on the operator’s display. If the operator declared every glitch in the noise an enemy plane, they’d scramble counter forces at every moment. But mistaking a plane for noise in the radar could be catastrophic. Hence, the cost of acting when there was no plane was high, the cost of not acting when there was a plane was significantly higher, but there was also the cost of action even if there was a plane. These factors could be weighted together to determine the correct threshold for when to be suspicious of ghost signals in the radar stream.

We can also use this decision framework to address the question from yesterday of whether to take Paxlovid after a negative covid test. In this case, the costs are much less cut and dry. Perhaps the only easy case here is that there’s no cost or benefit to not taking Paxlovid when you don’t have covid. But the other three boxes in our table are much more difficult to quantify. What is the reward of taking a medication when you have an illness? Most medications don’t work for everyone for all diseases. What is the cost of taking a medication when you don’t have an illness? If you’ve ever seen a drug commercial, you’ll know that “side effects may include…” a whole menagerie of unpleasant outcomes. What is the cost of not taking a medication when you are legitimately sick? For lots of treatments, including Paxlovid, the benefit over chicken soup and Netflix is marginal at best. 

Hmm. Decision-making might not be so cut and dry even if we can formulate a reasonable optimization problem. For most decisions, we still have a ton of uncertainty. Even probabilistic models are uncertain. Even in betting, this is a mess. We can compute odds for roulette, but what are the odds for the outcome of a sporting event? How precise can you be there? Not only is our ability to estimate odds suspect, but our ability to reliably model costs and benefits is also a challenge. Tomorrow, I want to discuss these aspects of uncertainty and how we might concretely quantify them.